Individual Mobility Prediction via Attentive Marked Temporal Point Processes

Individual Mobility Prediction via Attentive Marked Temporal Point Processes。代码：https://github.com/Kaimaoge/AMTPP_for_Mobility。结合深度学习的TPP，用注意力机制增强对事件的表示，使用混合ALL分布对事件间的时间间隔建模，通过学习OD转移概率矩阵给定O预测D。

预测用户下一个trip的开始时间$t$，起点$o$，目的地$d$。AMTPP模型用自注意力机制捕获用户travel behavior内的周期性和regularity。使用非对称的log-Laplace mixture distribution建模起始时间$t$的分布。此外，还开发了一个OD矩阵学习模块。

1 Introduction

本质上，用户的移动数据分为两类：带时间戳的位置序列$\{ (t_i, l_i) \}^n_{i=1}$，表示时间$t_i$的位置$l_i$；trip/activity sequence $\{(t_i, o_i, d_i)\}^n_{i=1}$，时间$t_i$的从$o_i$出发，目的地是$d_i$。预测下一位置的研究比较多，但是预测下一个trip的工作比较少。相比前者，后者的信息量更大，时空关联更复杂。而且trip记录比轨迹应用的场景更多。但是对OD建模，假设有$S$个位置，那就要$S \times S$这个数量级，考虑到时间和travel的方式，比如car, bike, bus、旅行的目的，work, school, leisure，这个数量级就更大了。

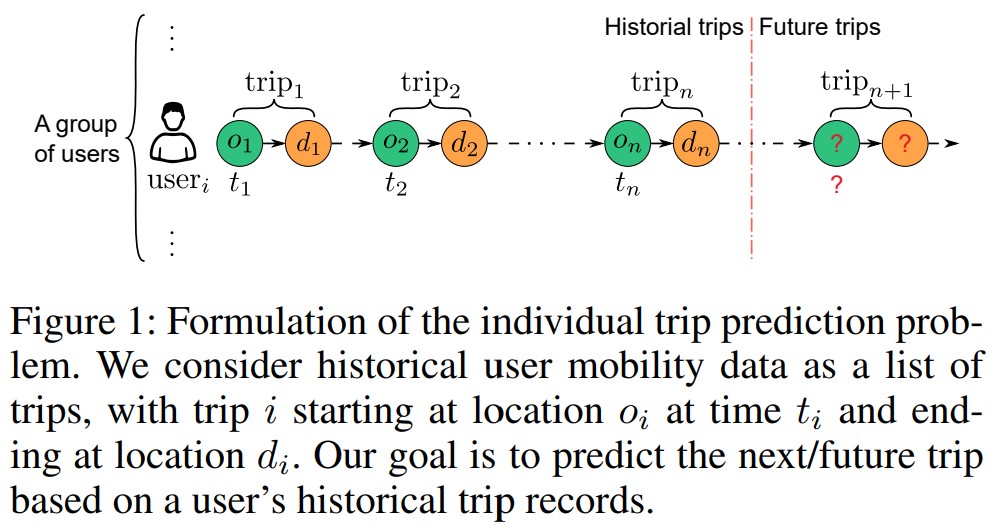
本文的目的是给定历史的轨迹$\{t_i, o_i, d_i\}^n_{i=1}$，预测$t_{n+1}, o_{n+1}, d_{n+1}$。如果把时间$t$看作是连续变量，$o, d$看作是离散变量，那么下一个trip的搜索空间是$[t_n, +\infty) \times \{1, \dots, S\} \times \{1, \dots, S\}$。现在处理事件序列的方法有两类：

1. HMM，隐马尔可夫模型
2. marked temporal point processes。

HMM的缺点是时间是离散的，不是连续的。TPP相比HMM，更通用。

最近的工作把深度学习和TPP结合在一起。但是这些方法在建模用户移动或旅行数据上有一些挑战。

1. OD数据之间的时空关系太复杂了。而且$S \times S$这个数量级太大。有些工作假设time和marker之间的关系是静态的。当marker的维数比较大的时候，参数会变得很多。
2. 很多TPP方法是用Hawkes过程来建模的，这种过程没法提现travel中的周期性。

本文提出的AMTPP解决了上述的挑战。用自注意力计算过去的trip对未来trip的影响。并且设计了一个新的position embedding来捕获时间信息。使用asymmetric Log-Laplace mixture distribution建模事件间的时间。ALL分布可以刻画travel behavior的rhythms和regularity。OD矩阵学习模块，可以从数据中学习到一个动态的OD关系矩阵。

Problem Description

一个用户$u$直到时间$t$的trip sequence：

$$\tag{1} \mathcal{H}^u_t = \{(t^u_1, o^u_1, d^u_1), \dots, (t^u_{n_u}, o^u_{n_u}, d^u_{n_u}): t^u_{n_u} \leq t \},$$

$n_u$表示序列中的trip个数。$t^u_i, o^u_i, d^u_i$表示第$i$个trip的出发时间、起点和目的地。时间是连续变量，OD是离散变量。后面忽略$u$。$t_i$可以表示为事件间的时间间隔$\tau_i = t_i - t_{i - 1} \in \mathbb{R}^+$。$\tau$可以看作是事件的活动时间。这俩表示是一样的。

目标：

$$\tag{2} p^\ast(\tau_{n+1}, o_{n+1}, d_{n+1}) = p(\tau_{n+1}, o_{n+1}, d_{n+1} \mid \mathcal{H}_{t_n}),$$

$\ast$表示条件概率。本文认为$o_{n+1} = d_n$，也就是上一个trip的目的地等于下一个trip的起点，这样的话，trip的TPP就变成普通的TPP了。

4 Methodology

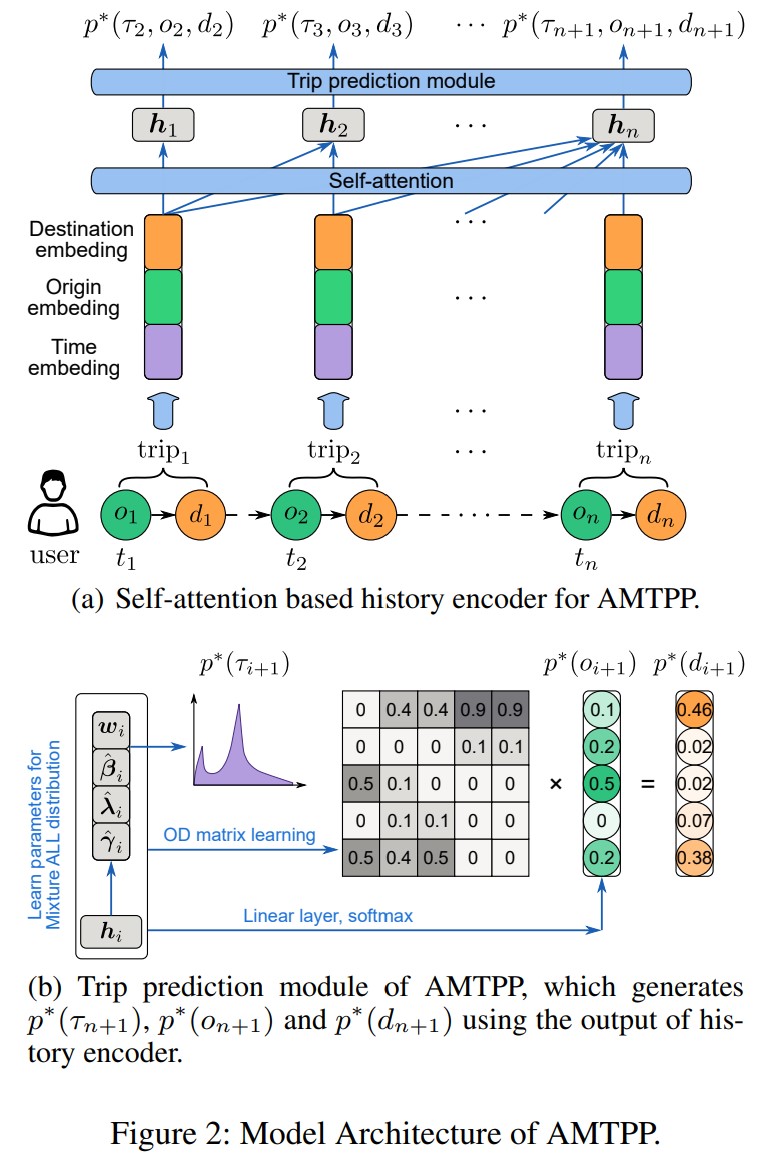
图2是AMTPP的架构。

4.1 Self-attention Encoder

第一步是获得$t_n, o_n, d_n$的嵌入表示：

$$\tag{3} e_n = \text{concat}(emb^t_n, emb^o_n, emb^d_n),$$

为了考虑周期和韵律，引入位置编码：

$$\tag{4} \begin{align} pe^n_n(pos_n, 2i) &= \text{sin}(pos_n / L^{2i/J}_{pos}),\\ pe^h_n(pos_n, 2i+1) &= \text{cos}(pos_n / L^{2i/J}_{pos}), \end{align},$$

$pos_n \in \{0, 1, \dots, 23 \}$是第$n$个trip的小时，$J$是嵌入的维数，$i \in \{1, \dots, \lfloor J/2 \rfloor \}$, $L_{pos}$是缩放因子。很多方法把$L_{pos}$设置成一个定值，比如10000，但是本文把它设定为一个参数。此外，还引入了day of week作为位置编码$pe^w_n$。加上$\tau_n$，最后的事件嵌入表示：

$$\tag{5} emb^t_n = \text{concat}(pe^w_n, pe^h_n, \tau_n).$$

OD嵌入：

$$\tag{6} \begin{align} emb^o_n &= \text{concat}(W^o_{em} \hat{o}_n + b^o_{em}, p^o_n),\\ emb^d_n &= \text{concat}(W^d_{em} \hat{d}_n + b^d_{em}, p^d_n), \end{align}$$

$W^o_{em} \in \mathbb{R}^{J_o \times S}, W^d_{em} \in \mathbb{R}^{J_d \times S}, b^o_{em} \in \mathbb{R}^{J_o}, b^d_{em} \in \mathbb{R}^{J_d}$是参数，$J_o, J_d$是OD嵌入向量的维数，$S$是位置的数量，$p^o_n, p^d_n$是OD的其他信息，比如POI什么的。

给定历史事件序列的嵌入$E_n = [e_1, e_2, \dots, e_n]^\top \in \mathbb{R}^{n \times J}$，用多头自注意力计算第$n$个trip的隐藏状态。注意力的参数矩阵$Q_l = EW^Q_l, K_l = E W^K_l, V_l = E W^V_l, l = 1, 2, \dots, L$。$W^Q_l, W^K_l \in \mathbb{R}^{J \times c_k}, W^V_l \in \mathbb{R}^{J \times C_v}$。

注意力：

$$\tag{7} \text{Att}(Q_l, K_l, V_l) = \text{softmax}(\frac{Q_l K^\top_l}{\sqrt{d_k}} \cdot M) V_l,$$

$M \in \mathbb{R}^{n \times n}$是mask矩阵，上三角部分设为$-\infty$，防止信息泄露。

多头注意力：

$$\tag{8} \begin{align} H &= \text{gelu}(\text{concat}(\text{head}_1, \dots, \text{head}_L) W^O),\\ \text{head}_l &= \text{Att}(EW^Q_l, EW^K_l, EW^V_l), \end{align}$$

$W_O \in \mathbb{R}^{L \cdot c_v \times C_{\text{model}}}$, $c_{\text{model}}$是输出的特征数。$\text{gelu}$表示Gaussian Error Linear Unit，非线性激活函数，$H_n = [h_1, h_2, \dots, h_n]^\top \in \mathbb{R}^{n \times c_{\text{model}}}$是输出。因为用了mask，所以$h_i$只是基于历史生成的。

4.2 Asymmetrical Log-Laplace Mixture for Inter-trip Time

这个部分是对事件间的时间间隔的条件概率分布 $p_\theta(\tau_{n+1} \mid h_n)$ 建模，使用参数为$\theta$的深度神经网络建模。《Intensity-Free Learning of Temporal Point Processes》这篇论文认为相比对强度函数建模，直接对时间间隔建模更方便。这篇论文用log-normal mixture model对TPP的条件概率密度$p_\theta(\tau_{n+1} \mid h_n)$建模。但是这个分布对trip之间的interval不适用，因为trip之间的interval表示了事件的持续时间，而且条件分布通常有一些明显的峰。为了更好的刻画trip间的时间间隔，本文用Aysmmetric Log-Laplace分布。这个分布经常用于对非常偏、有峰和长尾的数据建模。ALL分布有三个参数：

$$ALL(\tau; \beta, \lambda, \gamma) = \frac{\lambda \gamma}{\tau(\lambda + \gamma)} \begin{cases} (\frac{\tau}{\beta})^\lambda & \text{if} \ 0 < \tau < \beta,\\ (\frac{\beta}{\tau})^\gamma & \text{if} \ \tau \geq \beta, \end{cases}$$

$\beta$控制模式，$\lambda$和$\gamma$分别是左右长尾的正长尾参数。

理想的$p_\theta(\tau \mid h)$分布能趋近任意分布。因为混合模型有趋近$\mathbb{R}$上任意概率分布的性质：universal approximation(UA)，我们使用$\mathcal{D}$，作为ALL的混合分布，来趋近$p_\theta(\tau \mid h)$：

$$\tag{9} \mathcal{D}(\tau; w, \beta, \lambda, \gamma) = \sum^K_{k=1} w_k ALL(\tau; \beta_k, \lambda_k, \gamma_k),$$

$w$是混合权重。通过这个混合模型，我们可以近似一个用户的多模态旅行模式。举个例子，如果一个旅行者只有早上的通勤数据，我们在24小时内只能看到一个峰。但是对于来回通勤的人，我们希望看到的是早上一个峰，晚上一个峰。这种混合模型可以表示多个峰。

ALL混合分布下的变量的对数服从$\text{ALMixture}(w,\hat{\beta}, \hat{\lambda}, \hat{\gamma})$，每个部分是：

$$\tag{10} AL(y) = \frac{\hat{\lambda}_k}{\hat{\gamma}_k + \frac{1}{\hat{\gamma}_k}} \begin{cases} \exp (\frac{\hat{\lambda}_k}{\hat{\gamma}_k} (y - \hat{\beta}_k)) & \ \text{if} \ 0 < y < \hat{\beta}_k,\\ \exp(- \hat{\lambda}_k \hat{\gamma}_k (y - \hat{\beta}_k)) & \ \text{if} \ y \geq \hat{\beta}_k, \end{cases}$$

$\hat{\beta}_k = \log(\beta_k), \hat{\gamma}_k = \sqrt{\frac{\lambda_k}{\gamma_k}}, \hat{\lambda}_k = \sqrt{\lambda_k \gamma_k}$。

公式10里面的对数似然比公式9中的原始ALL更容易学习。我们用MDN网络学习ALMixture里面的参数：

$$\tag{11} \begin{align} w_n &= \text{softmax}(\Phi_w h_n + b_w),\\ \hat{\beta}_n &= \exp(\Phi_\beta h_n + b_\beta),\\ \hat{\lambda}_n &= \exp(\Phi_\lambda h_n + b_\lambda),\\ \hat{\gamma}_n &= \exp(\Phi_\gamma h_n + b_\gamma), \end{align}$$

softmax和exp用来约束分布的参数，$\Phi, b$都是learnable parameters。

4.3 OD Matrix Learning

显然OD和$t$是有关的，即$p^\ast(o_{n+1} \mid \tau_{n+1})$，这里我们没有直接对时间$\tau$建模，而是对$\tau$上面的参数$\{w_n, \beta_n, \lambda_n, \gamma_n \}$建模，这样就不用从分布中采样了。因为ALL混合分布中的参数是有物理意义的，从学习到的模型中模拟trip也很容易。通过调整参数就可以看到OD分布的变化。举个例子，减小峰参数$\beta$来观察OD分布的变化，可以理解成一个人的出发时间提前之后他的trip会有什么变化。

$$\tag{12} \begin{align} \hat{h}_n &= \text{concat}(h_n, w_n, \hat{\beta}_n, \hat{\lambda}_n, \hat{\gamma}_n),\\ \hat{o}_{n+1} &= \text{softmax}(\Phi_o \hat{h}_n + b_o), \end{align}$$

下一个位置$\hat{o}_{n+1}$的分布依赖拼接向量$\hat{h}_n$，这个向量由历史编码$h_n$和trip的时间参数组成。

$p^\ast(d_{n+1})$通过把$\hat{o}_{n+1}$乘以一个OD矩阵$OD_{n+1}$得到，这个矩阵的每一列包含了从一个O转移到所有D的转移概率。这个OD矩阵很有用，有了这个OD矩阵，我们可以知道地铁线路里面哪个结点的人比较多。但是$S \times S$太大了，学一个实时的OD矩阵太难了。我们用下面的方法学习OD_{n+1}里面的参数：

$$\tag{13} \begin{align} D^1_{n+1} &= \text{reshape}(\Phi^1_m \hat{h}_n),\\ D^2_{n+1} &= \text{reshape}(\Phi^2_m \hat{h}_n),\\ OD_{n+1} &= D^1_{n+1}{D^2_{n+1}}^\top \cdot M_{od},\\ OD_{n+1} &= \text{softmax}(OD_{n+1}).\\ \hat{d}_{n+1} &= OD_{n+1} \hat{o}_{n+1} \end{align}$$

$D^1_{n+1}, D^2_{n+1} \in \mathbb{R}^{S \times r}$, $r \ll S$。$\Phi$是learnable parameters。$M_{od} \in mathbb{R}^{S \times S}$用来过滤掉不可能的OD pair，方法就是把这些位置设置成 $- \infty$，包括矩阵的对角线。softmax用来约束矩阵的每一列的和都为1。这个矩阵是根据时间编码$\hat{h}_n$动态变化的。输出的$\hat{d}_{n+1}$和输入的$\hat{o}_{n+1}$与参数关联在一起，让网络训练起来更容易。

4.4 Model Training

负对数似然。随机梯度下降。短的序列要加pad。pad部分会被mask掉。损失函数：

$$\tag{14} \mathcal{L} = - \sum^U_{u=1} \sum^{n_u}_{n=1} \log p^\ast_\Theta(\tau^u_n) + \log p^\ast_\Theta(o^u_n) + \log p^\ast_\Theta(d^u_n),$$

$U$是用户数，$n_u$是用户$u$的trip的个数。对于$\tau$的对数似然，在$\tau$上面加一个对数变换，得到非对称Laplace分布：$y = \log(\tau)$，最终得到：

$$\tag{15} \begin{align} \log p^\ast_\Theta(\tau) &= \log p^\ast_\Theta(y) - \log(\tau), \ \ \ \ y = \log(\tau),\\ p^\ast_\Theta(y) &= \text{ALMixture}(w, \hat{\beta}, \hat{\lambda}, \hat{\gamma}). \end{align}$$