最近给本科生当机器学习课程的助教，给他们出的作业题需要看这些图，懒得放本地了，直接放博客里。发现jupyter导出markdown好方便，放到博客里面正好，改都不用改。

原来就想过一个问题，为什么我写出来的神经网络不收敛，loss会像火箭一样直接飞了。后来看了一些教程，发现有人在做梯度下降的时候，把梯度除以了梯度的二范数，我尝试之后发现还真好使了，在实验的时候发现是因为没有对数据集进行归一化，如果所有的数据都是很大的数，那么在反向传播的时候，计算出来的梯度的数量级会很大，这就导致更新得到的参数的数量级也很大，预测出的偏差就更大了，然后循环往复，如果给梯度除以一个梯度的二范数，其实就相当于把梯度的数量级降了，这样就可以训练了。但实际上还是将原始数据归一化比较好，对原始数据归一化还能让梯度下降的方向更多。如果数据都是正数，那下降方向会少很多，下降的时候会出现zig-zag现象。

第二题：神经网络：线性回归

实验内容：

学会梯度下降的基本思想
学会使用梯度下降求解线性回归
了解归一化处理的作用

线性回归

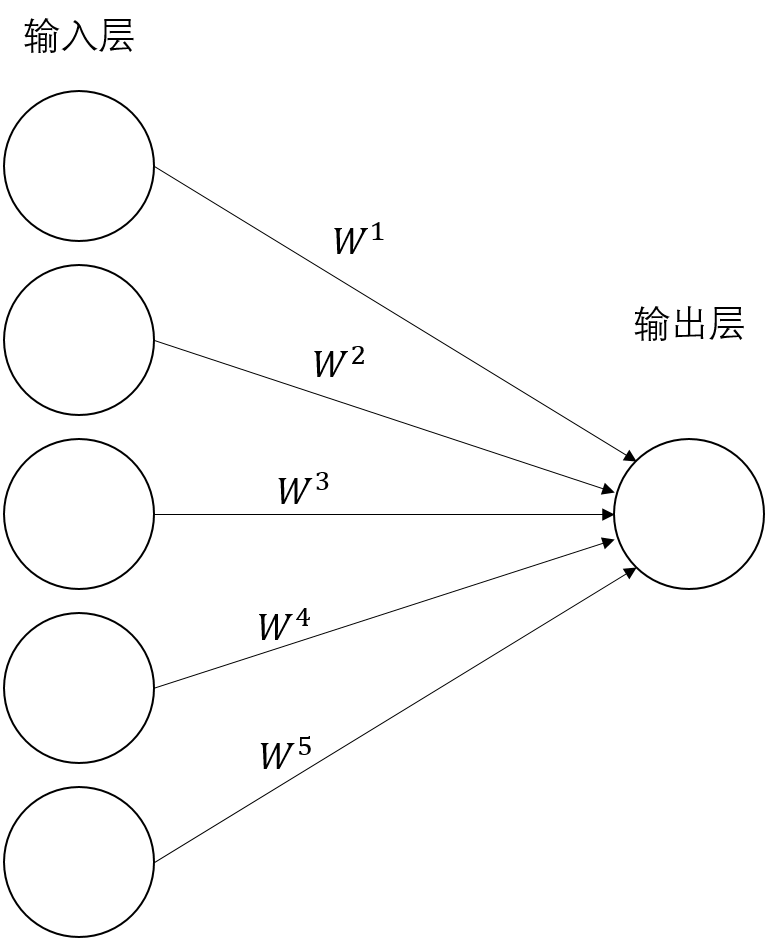
我们来完成最简单的线性回归，上图是一个最简单的神经网络，一个输入层，一个输出层，没有激活函数。
我们记输入为$X \in \mathbb{R}^{n \times m}$，输出为$Z \in \mathbb{R}^{n}$。输入包含了$n$个样本，$m$个特征，输出是对这$n$个样本的预测值。
输入层到输出层的权重和偏置，我们记为$W \in \mathbb{R}^{m}$和$b \in \mathbb{R}$。
输出层没有激活函数，所以上面的神经网络的前向传播过程写为：

$$ Z = XW + b $$

我们使用均方误差作为模型的损失函数

$$ \mathrm{loss}(y, \hat{y}) = \frac{1}{n} \sum^n\_{i=1}(y\_i - \hat{y\_i})^2 $$

我们通过调整参数$W$和$b$来降低均方误差，或者说是以降低均方误差为目标，学习参数$W$和参数$b$。当均方误差下降的时候，我们认为当前的模型的预测值$Z$与真值$y$越来越接近，也就是说模型正在学习如何让自己的预测值变得更准确。

在前面的课程中，我们已经学习了这种线性回归模型可以使用最小二乘法求解，最小二乘法在求解数据量较小的问题的时候很有效，但是最小二乘法的时间复杂度很高，一旦数据量变大，效率很低，实际应用中我们会使用梯度下降等基于梯度的优化算法来求解参数$W$和参数$b$。

梯度下降

梯度下降是一种常用的优化算法，通俗来说就是计算出参数的梯度（损失函数对参数的偏导数的导数值），然后将参数减去参数的梯度乘以一个很小的数（下面的公式），来改变参数，然后重新计算损失函数，再次计算梯度，再次进行调整，通过一定次数的迭代，参数就会收敛到最优点附近。

在我们的这个线性回归问题中，我们的参数是$W$和$b$，使用以下的策略更新参数：

$$ W := W - \alpha \frac{\partial \mathrm{loss}}{\partial W} $$$$ b := b - \alpha \frac{\partial \mathrm{loss}}{\partial b} $$

其中，$\alpha$ 是学习率，一般设置为0.1，0.01等。

接下来我们会求解损失函数对参数的偏导数。

损失函数MSE记为：

$$ \mathrm{loss}(y, Z) = \frac{1}{n} \sum^n\_{i = 1} (y\_i - Z\_i)^2 $$

其中，$Z \in \mathbb{R}^{n}$是我们的预测值，也就是神经网络输出层的输出值。这里我们有$n$个样本，实际上是将$n$个样本的预测值与他们的真值相减，取平方后加和。

我们计算损失函数对参数$W$的偏导数，根据链式法则，可以将偏导数拆成两项，分别求解后相乘：

这里我们以矩阵的形式写出推导过程，感兴趣的同学可以尝试使用单个样本进行推到，然后推广到矩阵形式

$$\begin{aligned} \frac{\partial \mathrm{loss}}{\partial W} &= \frac{\partial \mathrm{loss}}{\partial Z} \frac{\partial Z}{\partial W}\\ &= - \frac{2}{n} X^\mathrm{T} (y - Z)\\ &= \frac{2}{n} X^\mathrm{T} (Z - y) \end{aligned}$$

同理，求解损失函数对参数$b$的偏导数:

$$\begin{aligned} \frac{\partial \mathrm{loss}}{\partial b} &= \frac{\partial \mathrm{loss}}{\partial Z} \frac{\partial Z}{\partial b}\\ &= - \frac{2}{n} \sum^n\_{i=1}(y\_i - Z\_i)\\ &= \frac{2}{n} \sum^n\_{i=1}(Z\_i - y\_i) \end{aligned}$$

因为参数$b$对每个样本的损失值都有贡献，所以我们需要将所有样本的偏导数都加和。

其中，$\frac{\partial \mathrm{loss}}{\partial W} \in \mathbb{R}^{m}$，$\frac{\partial \mathrm{loss}}{\partial b} \in \mathbb{R}$，求解得到的梯度的维度与参数一致。

完成上式两个梯度的计算后，就可以使用梯度下降法对参数进行更新了。

训练神经网络的基本思路：

首先对参数进行初始化，对参数进行随机初始化（也就是取随机值）
将样本输入神经网络，计算神经网络预测值 $Z$
计算损失值MSE
通过 $Z$ 和 $y$ ，以及 $X$ ，计算参数的梯度
使用梯度下降更新参数
循环1-5步，在反复迭代的过程中可以看到损失值不断减小的现象，如果没有下降说明出了问题

接下来我们来实现这个最简单的神经网络。

1. 导入数据

使用kaggle房价数据，选3列作为特征

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

# 读取数据
data = pd.read_csv('data/kaggle_house_price_prediction/kaggle_hourse_price_train.csv')

# 使用这3列作为特征
features = ['LotArea', 'BsmtUnfSF', 'GarageArea']
target = 'SalePrice'
data = data[features + [target]]

2. 数据预处理

40%做测试集，60%做训练集

1
2
from sklearn.model_selection import train_test_split
trainX, testX, trainY, testY = train_test_split(data[features], data[target], test_size = 0.4, random_state = 32)

训练集876个样本，3个特征，测试集584个样本，3个特征

1
trainX.shape, trainY.shape, testX.shape, testY.shape

3. 参数初始化

这里，我们要初始化参数$W$和$b$，其中$W \in \mathbb{R}^m$，$b \in \mathbb{R}$，初始化的策略是将$W$初始化成一个随机数矩阵，参数$b$为0。

1
2
3
4
5
def initialize(m):
    '''
    参数初始化，将W初始化成一个随机向量，b是一个长度为1的向量
    
    Parameters