在训练神经网络的时候,normalization是必不可少的,原因是如果不进行normalization,在更新参数的时候会出现zig zag的现象。
在训练神经网络的时候,归一化是必不可少的。之前一直不理解为什么非要归一化,直到看了cs231n这门课才知道归一化的目的。
事实上这个问题主要是针对激活函数来说,如果不归一化的话,那么激活函数在反向传播的时候就会出问题。
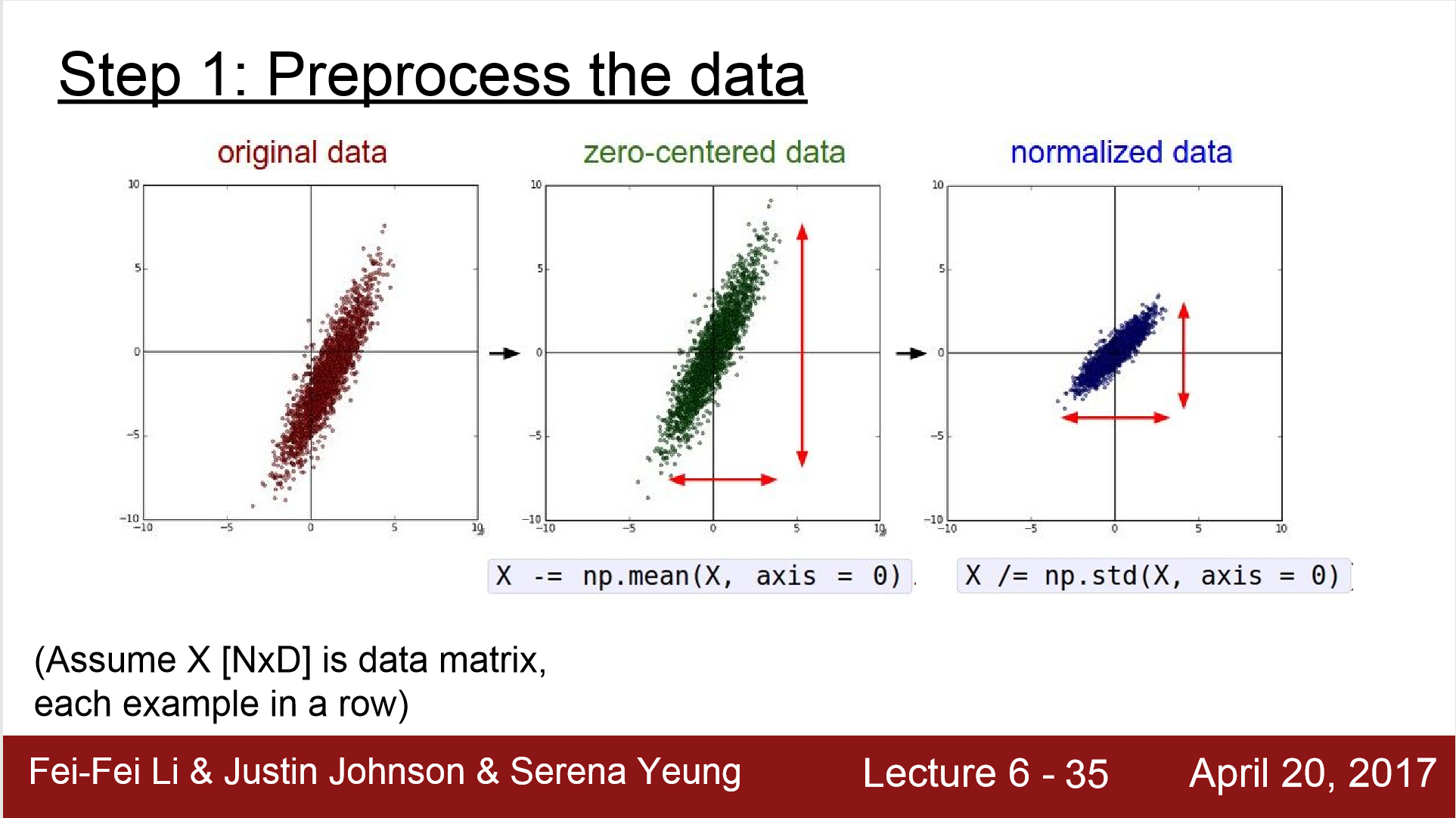 图1 左侧是原始数据,中间是中心化后的,右侧是归一化后的 图片来源于cs231n
事实上归一化分为两个步骤,第一步是将数据变为以0为中心,第二部是缩小数据的范围。所以归一化的公式为:
图1 左侧是原始数据,中间是中心化后的,右侧是归一化后的 图片来源于cs231n
事实上归一化分为两个步骤,第一步是将数据变为以0为中心,第二部是缩小数据的范围。所以归一化的公式为:
其中,X为原始样本,$\bar{X}$为样本均值,$std(X)$为样本标准差。 在这里,真正影响反向传播的是第一步,zero-centered。如果没有将数据以0为中心中心化的话,就会影响反向传播的效果。 以逻辑回归(Logistic Regression)为例,逻辑回归的模型可写为
$$\hat{y} = sigmoid(W \cdot X+b)$$其中$W$和$b$是参数,X是样本,$sigmoid$表示sigmoid激活函数,设损失函数为
$$L = Loss(y, \hat{y})$$其中,$y$为样本的标签或标注值。在反向传播的时候,需要对$W$和$b$求偏导数,即求损失函数在当前样本点的梯度,这里我们设$Z = W \cdot X + b$,则
$$\frac{\partial{L}}{\partial{W}} = \frac{\partial{L}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{Z}}\frac{\partial{Z}}{\partial{W}} = \frac{\partial{L}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{Z}}X^T$$同理可以求出$b$的偏导数。 在这里就可以看出问题,假设我们的输入是图像那样的样本,像素值都是大于0的,那这里$\frac{\partial{L}}{\partial{W}}$就会大于0。 使用梯度下降的更新规则来更新参数时
$$W := W - \alpha \frac{\partial{L}}{\partial{W}}$$W就会一直减小,这显然是有问题的。
 图2 右图展示了只有两个方向允许更新梯度后实际的参数更新路线(红线) 图片来源于cs231n
如图2所示,可以发现如果我们的输入变成了要么都是大于0,要么都是小于0的数,那么允许梯度更新的两个方向在二维空间中就只能落在第一和第三象限中,扩展到高维空间中也是相对的两个卦限。这样在更新的过程中就会产生这种红线所示的路径zig zag path。以上是不进行中心化的后果。
而不进行特征缩放的后果则是,如果每个特征的量级不同,假设一个特征是数值范围在$[-10, 10]$,另一个特征在$[-10^9, 10^9]$,那么在计算梯度后,使用梯度下降更新时,也会造成上面所述的zig zag现象。
图2 右图展示了只有两个方向允许更新梯度后实际的参数更新路线(红线) 图片来源于cs231n
如图2所示,可以发现如果我们的输入变成了要么都是大于0,要么都是小于0的数,那么允许梯度更新的两个方向在二维空间中就只能落在第一和第三象限中,扩展到高维空间中也是相对的两个卦限。这样在更新的过程中就会产生这种红线所示的路径zig zag path。以上是不进行中心化的后果。
而不进行特征缩放的后果则是,如果每个特征的量级不同,假设一个特征是数值范围在$[-10, 10]$,另一个特征在$[-10^9, 10^9]$,那么在计算梯度后,使用梯度下降更新时,也会造成上面所述的zig zag现象。