PVLDB 2022. DeepTEA: Effective and Efficient Online Time-dependent Trajectory Outlier
Detection

Abstract

研究异常轨迹检测，目的是提取道路中车辆的异常移动。可以帮助理解交通行为，识别出租车欺诈。由于交通状况在不同时间不同地点会发生变化，所以这个问题具有挑战。本文提出了Deep-probabilistic-based time-dependent anomaly detection algorithm (DeepTEA)。使用深度学习方法从大量轨迹里面获得time-dependent outliners，可以处理复杂的交通状况，并精确地检测异常现象。本文还提出了一个快速的近似方法，为了在实时环境下捕获到异常行为。相比SOTA方法，本文方法提升了17.52%，并且可以处理百万计的轨迹数据。

2. Problem Definition

Definition 1(Trajectory). 轨迹点$p_{t_i}$是一个三元组$(t_i, x, y)$，分别是时间戳、纬度、经度。轨迹$T$是一个轨迹点的有序序列，其中$t_1 < \dots < t_i < \dots < t_n$。

轨迹异常检测分为两类，一类是只考虑与正常路线不同的异常轨迹。另一种是考虑与time-dependent的正常路线不同的异常轨迹。

Definition 2(Time-dependent Trajectory Outlier)。给一条轨迹$T$，起点$S_T$，终点是$D_T$，还有travel时间，一个time-dependent轨迹异常定义为：相同的$S_T$和$D_T$以及相同的出发、到达时间下的轨迹里面，一个很稀有的、不同于其他轨迹的轨迹。

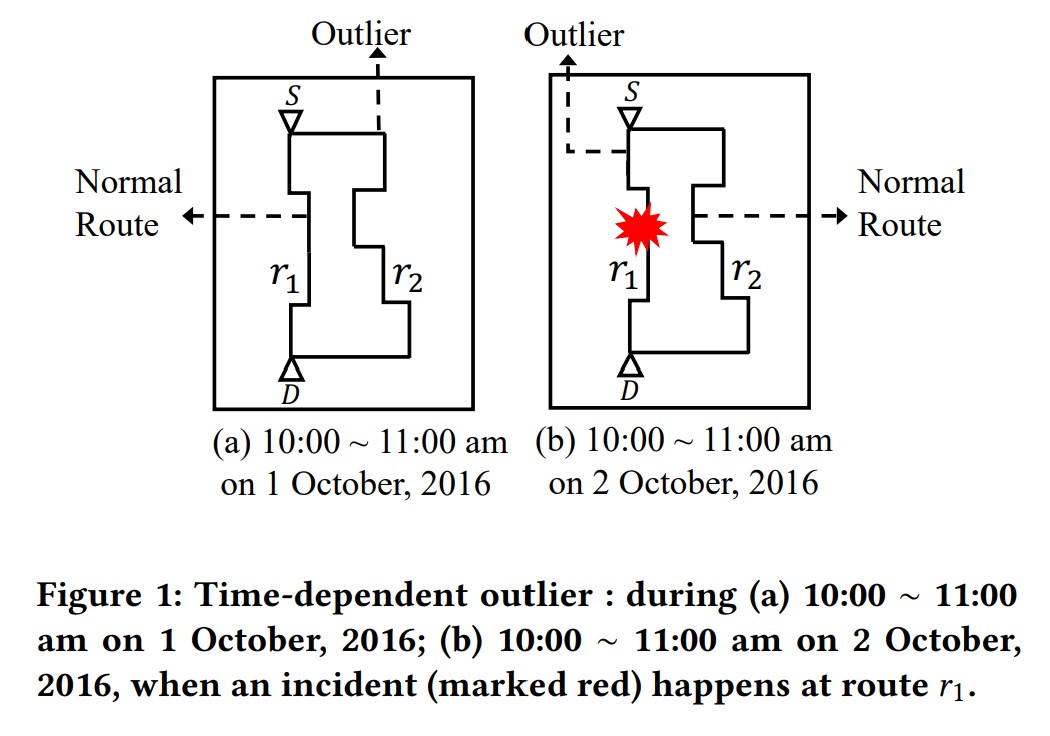
举例，如果一个轨迹在2016年10月1日的上午10点出发，11点到达，那么一条稀有的轨迹且和相同时间相同OD的轨迹不同的轨迹就是这个Time-dependent Trajectory Outlier.

Problem 1(Online Time-dependent Trajectory Outlier Detection)。给定一条正在前进的轨迹$T$，实时计算并更新这条轨迹是时间依赖的异常轨迹的概率。

3. The DeepTEA Model

3.1 Framework

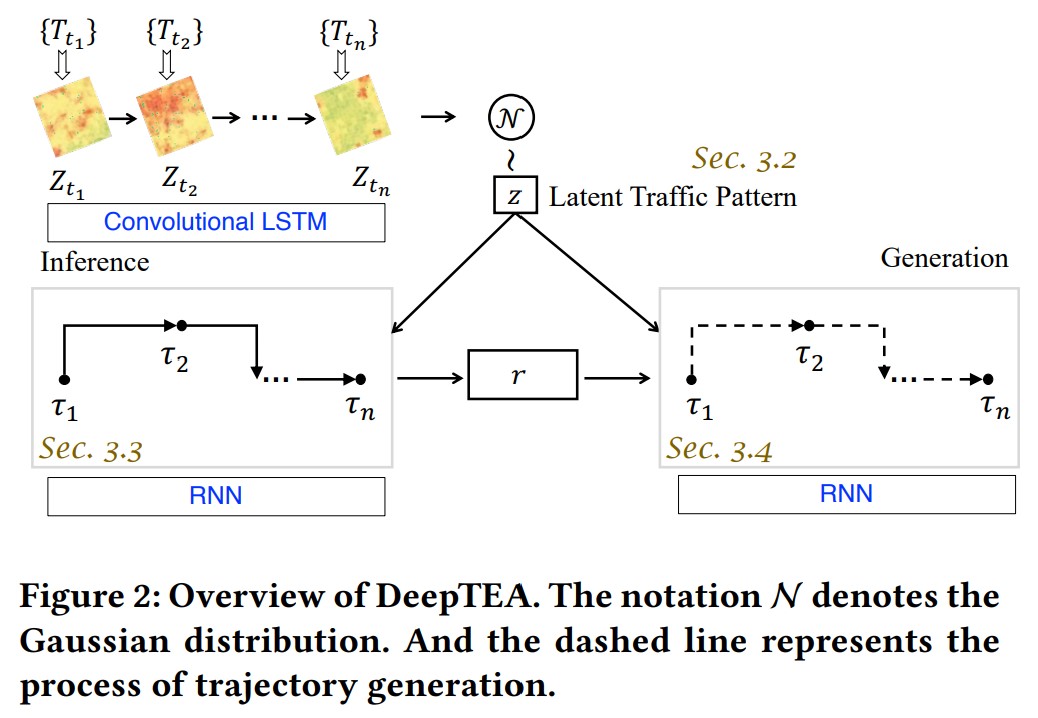
给定轨迹$T$，在旅行过程中推算latent traffic pattern $q(z \mid T)$。轨迹观测值 $\tau$ 反映时间依赖的轨迹转移，可以在 inference network 里面用来建模latent time-dependent route $r$。之后，time-dependent route $r$用来生成轨迹观测值$\tau$。

3.2 Latent Traffic Pattern Inference

latent traffic pattern $z$，表示旅途过程中的动态交通状况，比如 ${\text{smooth} \rightarrow \text{congested} \rightarrow \text{smooth} }$，或者${\text{congested} \rightarrow \text{smooth} }$。

3.2.1 Challenges

给定轨迹 $T$，我们想基于 $T$ 的空间转移，推算出 latent traffic pattern $q(z \mid T)$。举个例子，一个远距离的移动表明当时的交通状况是通畅的。但是一个轨迹 $T$ 可能表示一些随机行为，比如停车休息，这种行为不能表明当时的交通状况。这是在表示实际交通模式时的第一个挑战。第二个挑战是交通状态在不同的地方，不同的时间是不同的，动态的。同一时间，不同OD也是不一样的。而且在整个旅途中的交通状态变化也是剧烈的。可能开始的时候顺畅，结束的时候拥堵。捕获交通状态很重要，因为它对时间依赖的正常路径影响很大。

3.2.2 Design

为了解决第一个挑战，我们从时间 $t_i$ 的一组轨迹 ${ T_{t_i} }$ 里面学习latent traffic pattern $z$，而不是单条轨迹 $T$。这里我们用 time point series 表示旅行时间。为了从 ${ T_{t_i} }$ 里面很好地组织交通信息，我们使用一个 map grid matrix $Z_{t_i}$，这里面每个单元表示平均速度，用这个对 $t_i$ 的交通状态建模。从图2可以看出，红色表示速度低，表示拥堵。绿色表示畅通。黄色表示即将拥堵，平均速度介于红绿之间。为了解决同一时间不同位置交通状态的多样性，我们用CNN建模。对于没有车辆的区域，CNN可以从有车辆的单元学到信息，而不是将他们表示为缺失值。因为实时状态下交通状况变得很频繁，我们用RNN捕获这种不断变化的动态性，解决第二个挑战。交通状态的变化可以通过RNN很好的建模。然后我们用一个高斯分布和RNN的隐藏状态，推算 latent traffic pattern $z$。CNN+RNN选用了 Convolutional LSTM。

我们用上面的随时间变化的动态交通状态来推算latent traffic pattern $z$。这里的想法是交通状态会因为复杂的实时特征发生变化，比如信号灯、事故、早晚高峰。因此，我们在DeepTEA里面会随时间变化更新$Z$，表示为$Z_{t_i}$，表示轨迹点$p_{t_i}$在时间$t_i$的交通状态。我们会从实际交通状况$Z = { Z_{t_i}, Z_{t_{i+1}}, \dots, Z_{t_{i+n}} }$里面推算latent traffic pattern $z$。这里面的交通状况对应的时间分别是对应轨迹点${ p_t, p_{t+1}, \dots, p_{t_{i+n}} }$的时间。对于真实交通状况$Z$，我们可以得到轨迹$T$经过的时间的平均速度。换句话说就是，真实交通状况$Z_{t_i}$是一个平均速度矩阵，它包含了整个城市在$t_i$的移动状态。如果两个轨迹点之间的时间差很小，那么$Z_{t_i}$和$Z_{t_{i+1}}$可能会很相似。这样的话，我们需要把速度按时段提前聚合起来，就取平均速度，比如10分钟的时段，而不再使用时间点。为了减轻稀疏的问题，我们使用CNN将有车辆的位置的信息传播到没有车辆没数据的位置上。为了捕获不同时段的动态变化，我们用RNN建模时间维度的交通转移。这样，spatial traffic correlation和temporal transition通过$f_1(Z)$来捕获：

$$ \tag{1} f\_1(Z) = \text{RNN}(\text{CNN}(Z)), $$

这里函数$f_1(\cdot)$是一个CNN+RNN，CNN对每个$Z_i$都使用，然后用RNN对他们建模，捕获traffic transition。

为了让模型具有生成能力，并且对交通状态的不确定性建模，在给定实际交通状态$Z$的时候，我们用高斯分布对latent traffic pattern $z$建模，可以用来在给定轨迹$T$时近似latent traffic pattern $z$的分布，如公式2所示。我们将参数记为$\phi$，

$$ \tag{2} q\_\phi(z \mid T) \coloneqq q\_\phi(z \mid Z) = \mathcal{N}(\mu\_Z, \text{diag}(\sigma^2\_Z)), $$

均值$\mu_Z$和标准差$\sigma_Z$通过MLP函数 $g_1(f_1(Z))$得到，参数是$\phi = { f_1(\cdot), g_1(\cdot) }$。

这种方式在给定轨迹$T$的时候可以很好的推断出latent traffic pattern $z$。在训练阶段，参数$\phi$可以学到如何捕获latent traffic pattern $z$，而且能表示交通状态的多样性和动态性。

3.3 Latent Time-dependent Route Inference

3.3.1 Challenges

轨迹$T$不仅可以表示位置信息，还可以表示两个轨迹点之间转移的latent traffic pattern $z$。相比只最大化位置信息的似然，对位置和latent traffic pattern $z$同时做更informative，因为它可以反映在时间依赖的交通状态下的轨迹转移。

3.3.2 Design

一条轨迹 $T$ 不仅能反映位置 $p_{t_i}$，还能基于两个连续轨迹点 $p_{t_{i-1}}$ 和 $p_{t_i}$ 之间的转移，传递出 latent traffic pattern $z$。这里我们用 $o(p_{t_i}, z)$ 表示轨迹 $T$ 背后的观测值 $\tau_i$。这里希望用一个神经网络处理观测值 $p_{t_i}$ 和 $z$：

$$ \tag{3} \tau\_i = o(p\_{t\_i}, z) = f\_2(p\_{t\_i}, z) = \text{NN}(p\_{t\_i}, z), $$

我们使用一个神经网络学习 latent traffic pattern $z$ 的观测值 $p_{t_i}$：

$$ \tag{4} \text{NN}(p\_{t\_i}, z) = W p\_{t\_i} + Q z, $$

$\text{NN}$的参数是$W$和$Q$。

然后，我们学习一条轨迹 $T$ 经过的 latent time-dependent route $r$。我们解释过，轨迹 $T$ 不仅能表示轨迹点 $p_{t_i}$ 的位置信息，还能指明两个轨迹点之间转移的 latent traffic pattern $z$。latent time-dependent route $r$ 的含义可以解释为：高峰时间段城市路段的交通状态是拥堵的，驾驶员通常会上高速，因为那里会畅通。

轨迹 $T$ 经过的 latent time-dependent route $r$ 的表示为：

$$ \tag{5} r\_T \sim q\_\gamma (r \mid T), $$

$\gamma$ 是推测 latent time-dependent route $r$ 时的参数。

基于之前的轨迹点和 latent traffic pattern $z$，我们可以用RNN获得轨迹观测值之间的转移，RNN记为 $f_3$，这里使用GRU：

$$ \tag{6} h\_i = f\_3 (h\_{i-1}, \tau\_i), $$

$h_{i-1}$ 是之前观测值 $\tau_{i-1}$ 的隐藏状态，也就是轨迹点 $p_{t_{i-1}}$ 带着 latent traffic pattern $z$。

对于轨迹观测值的不确定性，我们通过高斯分布建模 $q_\gamma (r \mid T)$：

$$ \tag{7} q\_\gamma (r \mid T) = \mathcal{N} (\mu\_T, \text{diag}(\sigma^2\_T)), $$

我们用一个神经网络 $g_3(h_n)$ 来学习均值和标准差。

为了在 latent traffic pattern 里面区分正常的轨迹转移和异常的轨迹转移，需要设计一个模块对轨迹里 latent time-dependent normal route建模，这里 $z$ 会提供 time-dependent traffic 信息。使用高斯分布：

$$ \tag{8} p\_\gamma (r \mid k, z) = \mathcal{N}(\mu\_r, \text{diag}(\sigma^2\_r)), $$

$k$ 表示 latent time-dependent route 的类型，服从多项式分布：

$$ \tag{9} p\_\gamma (k) = \text{Mult} (\pi), $$

$\pi$ 是多项式分布的参数。然后，趋近 $q_\gamma (r \mid T)$ 的均值的 latent time-dependent route 是time-dependent normal route。

然后，推断网络可以从给定的轨迹 $T$ 里面推算 latent time-dependent route $r$，latent time-dependent route type $k$，还有 latent traffic pattern $z$ 为 $q_{\gamma,\phi}(r, k, z \mid T)$。通过使用 mean-field approximation，可以分解为：

$$ \tag{10} q\_{\gamma,\phi}(r, k, z \mid T) = q\_\gamma(r \mid T) \ q\_\phi(z \mid T) \ q\_\gamma (k \mid T), $$

$q_\gamma (k \mid T)$ 可以转换为在给定轨迹 $T$ 经过 latent time-dependent route $r$ 的条件下，route type $k$ 的分布：

$$ \tag{11} q\_\gamma (k \mid T) \coloneqq p\_\gamma (k \mid r\_T) = \frac{p\_\gamma (k) p\_\gamma (r\_T \mid k)}{\sum^K\_{i=1} p\_\gamma (k\_i) p\_\gamma (r\_T \mid k\_i)}, $$

$K$ 是一个超参数，表示 route 类型的个数。

因此，推断网络可以从轨迹 $T$ 的观测值 $o(p_{t_i}, z)$ 推断出 latent time-dependent route $r$。$\gamma = { f_2(\cdot), f_3(\cdot), g_3(\cdot), \pi, \mu_r, \sigma_r }$ 这些都是参数。

3.4 Trajectory Observation Generation

生成轨迹观测值的目标是给定 latent time-dependent route $r$，time-dependent route type $k$ 和 latent traffic pattern $z$ 时，最大化生成轨迹观测值 $\tau_i$ 的概率，也就是 $o(p_{t_i}, z)$。这个概率记为 $p_\theta (T \mid r, z, k)$，$\theta$ 表示用于生成过程的参数。从对称的角度来看，我们用RNN来生成轨迹观测值 $\tau_i$，也就是 $o(p_{t_i}, z)$：

$$ \tag{12} \begin{align} \eta\_i &= f\_4 (\tau\_i, \eta\_{i-1}) \\ &= f\_4(o(p\_{t\_i}, z), \eta\_{i-1}) \\ &= \text{RNN} (o(p\_{t\_i}, z), \eta\_{i-1}), i = 1, 2, \dots, n, \ and \ \eta\_o = r, \end{align} $$

RNN的起始输入是 $\eta_0$。从 $\eta_1$ 开始，输入变成上一个隐藏状态 $\eta_{i-1}$ 和轨迹观测值 $o(p_{t_i}, z)$。因此，观测值 $\tau_i$，也就是 $p_{t_i}$ 在 latent traffic pattern $z$ 的时候，可以通过下面的公式生成：

$$ \tag{13} \begin{align} \tau\_i &= o(p\_{t\_i}, z) \sim p\_\theta (o(p\_{t\_i}, z) \mid o(p\_{1:i-1}, z), r) \\ &= p\_\theta(\tau \mid \eta\_{i-1}) \\ &= \text{Mult}(\text{softmax}(g\_4 (\eta\_{i-1}))), \end{align} $$

$g_4(\cdot)$是一个函数，把输出映射到网格的个数。softmax 用来把概率的和变成1。然后轨迹观测值 $\tau_i$ 可以通过多项式分布生成。

因此，轨迹观测值 $\tau_i$，也就是 $o(p_{t_i}, z)$，可以基于 latent time-dependent route $r$，route type $k$ 和 latent traffic pattern $z$ 生成。我们给生成用的参数记为 $\theta = { f_4(\cdot), g_4(\cdot) }$。这些参数会在训练的过程中学到。

3.5 Optimization

我们上面讲了，轨迹观测值不仅能反映位置信息，还能基于两个连续的轨迹点的转移传递出 latent traffic pattern。因此，目标函数是最大化观测到的轨迹的边缘对数似然：

$$ \tag{14} \log p\_\theta(T^{(1)}, T^{(2)}, \dots, T^{(N)}) \coloneqq \log p\_\theta (\tau^{(1)}, \tau^{(2)}, \dots, \tau^{(N)}). $$

我们通过最大化ELBO来优化上面的边缘对数似然函数：

$$ \tag{15} \log p\_\theta (T) \geq \text{ELBO} = \mathcal{L}(\phi, \gamma, \theta; T). $$

轨迹 $T$ 的边缘对数似然函数的 ELBO 通过下面的公式计算：

$$ \tag{16} \begin{align} \mathcal{L}(\phi, \gamma, \theta; T) &= \mathbb{E}\_{q\_{\gamma, \phi}(r, k, z \mid T)}[ \log \frac{p\_{\phi, \gamma, \theta}(r, k, z, T)}{q\_{\gamma, \theta}(r, k, z \mid T)}] \\ &= - \mathbb{E}\_{q\_\gamma(r \mid T)} D\_{KL} (q\_\gamma (k \mid T) \Vert p\_\gamma (k)) \\ & - \mathbb{E}\_{q\_\gamma (k \mid T)} D\_{KL} ( q\_\gamma (r \mid T) \Vert p\_\gamma (r \mid k, z)) \\ & - D\_{KL} (q\_\phi (z \mid T) \Vert p\_\phi(z)) + \mathbb{E}\_{q\_{\gamma, \phi}(r, k, z \mid T)} \log p\_\theta (T \mid r, z, k), \end{align} $$

其中，$p_\theta(z)$ 是 latent traffic pattern $z$ 的先验概率。生成网络 $\log p_\theta(T \mid r, z, k)$ 可以通过下面公式计算：

$$ \tag{17} \log p\_\theta (T \mid r, z, k) = \sum^n\_{i=1} \log p\_\theta (\tau\_i \mid \tau\_{1: i-1}, r, z, k) $$

整个训练过程的算法如算法1所示。在训练过程中，模型参数通过优化轨迹 $T$ 的 ELBO 来学习。然后这些学到的参数会用于 online anomaly detection，后面会介绍。

Algo1

3.6 Complexity Analysis

训练 DeepTEA 的复杂度是 $O(N \cdot (d_{Z_1} d_{Z_2} \bar{V} + \bar{n}))$，$N$ 是轨迹数，$d_{Z_1}$ 和 $d_{Z_2}$ 是 $Z$ 的大小，$\bar{V}$ 是时间间隔的平均个数，$\bar{n}$ 是轨迹的平均长度。

Online Trajectory Outlier Detection by DeepTEA

基于算法1学习得到的参数，当下一个轨迹观测值 $\tau_{i+1}$ 实时过来的时候，异常分数会实时更新。这个过程要快。而且直到轨迹完成，这个异常分数都要更新。

4.1 Online Detection by Generation

图3展示了在线异常轨迹检测的步骤。

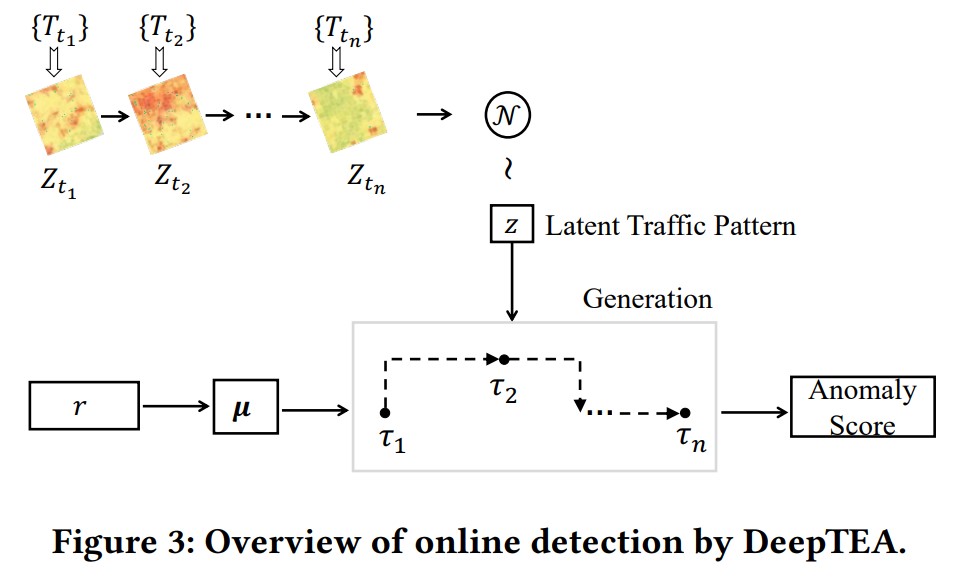
我们通过学到的网络生成观测到的轨迹来检测异常。latent time-dependent route 的分布 $q_\gamma (r \mid T)$ 可以通过参数 $\gamma$ 来计算。latent traffic pattern $z$ 可以通过参数 $\phi$ 和 $Z$ 获得。给定 $q_\gamma (r \mid T)$ 里面第 $k$ 个均值 $u_k$，我们用 RNN 生成轨迹观测值：

$$ \tag{18} \eta\_i = f\_4(\tau\_i, \eta\_{i-1}) = \text{RNN} (\tau\_i, \eta\_{i - 1}), i = 1, 2, \dots, n, \text{and} \ \eta\_0 = u\_k, $$

RNN的起始输入是 $\eta_0$，这里设置为 $u_k$。从 $\eta_1$ 开始，输入标称隐藏状态 $\eta_{i-1}$ 和轨迹观测值 $\tau_i$，即 $o(p_{t_i}, z)$。因此 $\tau_{i+1}$ 可以用下面的公式生成：

$$ \tag{19} p\_\theta (\tau\_{i+1} \mid \tau\_{i:i}, u\_k) = \text{softmax}(g\_4 (\eta\_{i-1})), $$

$g_4(\cdot)$ 是用来把输出映射到网格数的函数。

给定学到的 $q_\gamma (r \mid T)$ 和 latent traffic pattern $z$，轨迹 $T$ 的实时异常分数 $s_a(\tau_{i:i})$ 可以计算为 1 - 生成轨迹观测值 $\tau_{i:i}$ 的似然，即 ${ \tau_1 \rightarrow \tau_2 \rightarrow \dots \tau_i }$：

$$ \tag{20} s\_a(\tau\_{i:i}) = 1 - \arg \max\_k \exp [\frac{\sum^n\_{i=1} \log p\_\theta (\tau\_i \mid \tau\_{1:i-1}, u\_k)}{n}] $$

在线上场景下，给定之前的轨迹观测值 $\tau_{i:i}$，下一个轨迹观测值的异常分数可以通过之前这个数来计算：

$$ \tag{21} s\_a(\tau\_{i:i+1}) = 1 - \arg \max\_k \exp [\frac{\log p\_\theta (\tau\_{1:i} \mid u\_k) p\_\theta(\tau\_{i+1} \mid \tau\_{1:i}, u\_k)}{i + 1}] $$

Algo2

算法2是在线检测的过程。输入是轨迹 $T$，参数是从算法1学到的。对于新来的轨迹观测值 $\tau_{i+1}$，如果 latent traffic pattern $z$ 变了，那我们就更新 $z$。然后基于 $\tau_{1:i}$ 计算 $\tau_{1:i+1}$。最后返回异常分数。

4.2 Complexity Analysis

整个检测的复杂度是 $\mathcal{O}(d_{Z_1} d_{Z_2})$，$d_{Z_1}$ 和 $d_{Z_2}$ 是 $Z$ 的大小。

5 The DeepTEA-A Model: Approximate Online Detection

5.1 Approximation Algorithm

5.1.1 Challenge

基于 $\tau_{1:i}$ 的异常分数更新依赖 $t_{i+1}$ 的交通状态矩阵 $Z$，如果路网很大，这里耗时会长。

5.1.2 Design

受 GM-VSAE 的启发，本文提出了近似算法。使用 $\tau_1$ 的时段的交通状态矩阵 $Z$ 作为整个 trip 过程的交通状况的近似。这样，$Z$ 只要在第一个轨迹观测值 $\tau_1$ 的时候算一下就好了。online 更新的时候就不需要再算这个了。

给定一个起点 $S_T$ 和终点 $D_T$，从 $q(k \mid S_T, D_T, z_{S_T})$ 这里面取出最优的 latent route type $k$ 来近似最有 latent route pattern $u_k$，这需要从 $q_\gamma (r \mid T)$ 的 $k$ 个均值里面找，$Z_{S_T}$ 是 trip 开始时的交通状况。这样，最优的 latent route type $k$ 在 trip 一开始的时候就能拿到。从第二个轨迹观测值开始，这个 $k$ 就不需要再算了。

对于起点 $S_T$，交通状况 $Z_{S_T}$ 的隐藏状态可以通过下面公式计算：

$$ \tag{22} f\_1(Z\_{S\_T}) = \text{CNN} (Z\_{S\_T}), $$

然后 $z_{S_T}$ 可以从 $q_\phi (z_{S_T} \mid Z_{S_T})$ 里面采样得到：

$$ \tag{23} q\_\phi (z\_{S\_T} \mid Z\_{S\_T}) = \mathcal{N}(\mu\_{Z\_{S\_T}}, diag(\sigma^2\_{Z\_{S\_T}})), $$

然后，$\tau_{S_T}$ 可以通过 $f_2(\cdot)$ 得到：

$$ \tag{24} \tau\_{S\_T} = f\_2(S\_T, z\_{S\_T}) = \text{NN}(S\_T, z\_{S\_T}) = W S\_T + Q z\_{S\_T}, $$

同理，$\tau_{D_T}$ 按同样的方式计算。

然后 $q(k \mid S_T, D_T, z_{S_T})$ 通过 MLP 计算：

$$ \tag{25} q(k \mid S\_T, D\_T, z\_{S\_T}) = \text{softmax}(f\_t(\tau\_{S\_T}, \tau\_{D\_T})), $$

$f_5$ 就是 MLP。参数记为 $\delta = { f_5 (\cdot) }$。

公式20里面，为了获得最优的 $k$，需要跑 $k$ 次。一个简单的方法是通过 $q_\gamma (k \mid T)$ 从轨迹 $T$ 里面找到最优的 $k$。因此 $q(k \mid S_T, D_T, z_{S_T})$ 和 $q_\gamma (k \mid T)$ 要尽可能的相近。我们用交叉熵最小化两个分布的差别：

$$ \tag{26} l\_k = - \sum^K\_{k=1} q\_\gamma (k \mid T) \log q(k \mid S\_T, D\_T, z\_{S\_T}), $$

这个交叉熵 $l_k$ 会和公式 16 的ELBO同时训练。然后在线检测阶段的时候，最优的 $k$ 是 $q(k \mid S_T, D_T, z_{S_T})$ 里面最高概率的那个。然后直接就能拿到最优 latent time-dependent route $u_k$。

需要注意的是，近似算法的训练过程和算法1不一样。首先，交通状况的使用不一样，近似算法只用了 $Z_{S_T}$。第二，公式26，是一个 co-training 过程，为了近似两个分布。训练后得到模型参数 $\phi, \gamma, \theta, \delta$。整个训练过程如算法3所示。先从 $Z_{S_T}$ 里面获得 $z_{S_T}$。然后获得最优的 latent time-dependent route $u_k$，这个数只要在轨迹开始的时候算一下就好了。然后基于 $p_\theta(\tau_{1:i} \mid u_k)$ 更新异常分数就好了。

5.2 Complexity Analysis

在线检测的复杂度 $\mathcal{O}(d_{h_t}(d_{h_t} + d_{\tau_i}))$。这项是新的轨迹观测值 $\tau_{i+1}$ 到来的时候 RNN 的变换过程的复杂度。因为 $d_{h_t}, d_{\tau_i}$ 是常数，所以近似算法的复杂度是 $\mathcal{O}(1)$