NIPS 2019: Fully Neural Network based Model for General Temporal Point Processes。创新点是之前的条件强度函数有一个积分项,这个积分项不是很好求,本文提出用一个FNN计算累积强度函数,这样条件强度函数的计算只需要计算累积强度函数对事件时间间隔的偏导数就可以得到了。代码:https://github.com/omitakahiro/NeuralNetworkPointProcess
2 Method
条件强度函数:
$$ \tag{5} \lambda(t \mid H\_t) = \phi(t - t\_i \mid h\_i) $$这里$\phi$是非负函数,表示hazard函数。
Du et al., 2016提出的近似形式:
$$ \tag{6} \phi(\tau \mid h\_i) = \exp{(w^t \tau + v^\phi \cdot h\_i + b^\phi)} $$对数似然函数:
$$ \tag{8} \log{L(\{ t\_i \})} = \sum\_i[ \log{\phi(t\_{i+1} - t\_i \mid h\_i)} - \int^{t\_{i+1} - t\_i}\_0 \phi(\tau \mid h\_i)d\tau] $$使用BPTT优化,$h_i$是RNN的隐藏状态。
2.4 Proposed Model
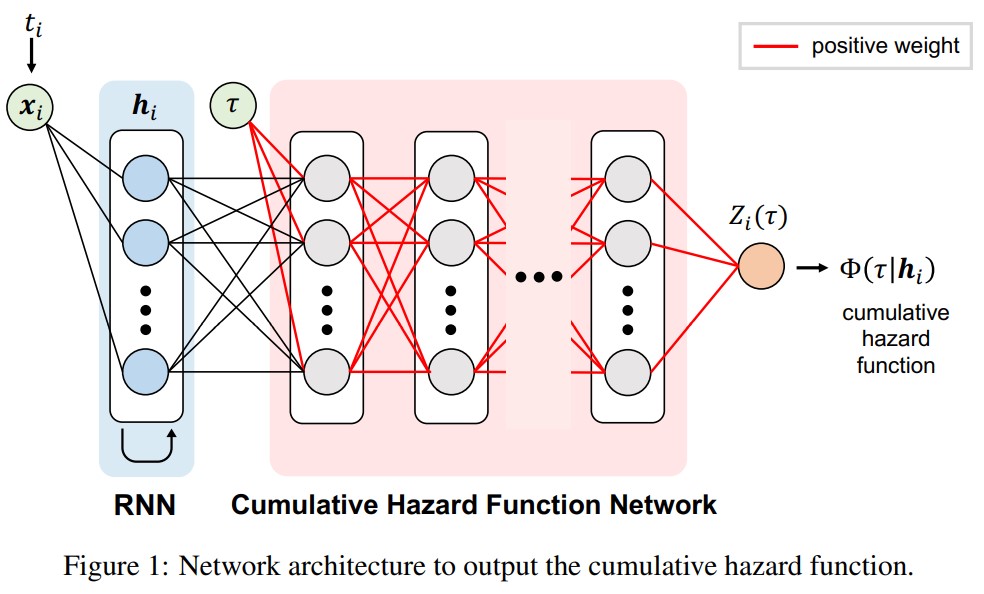
这里建模累积hazard函数:
$$ \tag{9} \Phi(\tau \mid h\_i) = \int^\tau\_0 \phi(s \mid h\_i)ds $$hazard函数通过对上式求偏导数得到:
$$ \tag{10} \phi(\tau \mid h\_i) = \frac{\partial}{\partial \tau} \Phi(\tau \mid h\_i) $$对数似然函数可以改写为:
$$ \tag{11} \log{L(\{t\_i\})} = \sum\_i[\log{\{\frac{\partial}{\partial \tau} \Phi(\tau = t\_{i+1} - t\_i \mid h\_i)\}} - \Phi(t\_{i+1} - t\_i \mid h\_i)] $$累积Hazard函数是一个关于$\tau$的正的单调递增函数。本文用一个FNN网络近似这个函数。为了保证这个性质,只要在$\tau$到最后的损失的路径上权重都是正的就好了。网络架构如图1所示。在模型参数更新的时候,如果权重变成负的,就用绝对值替换它。
这里看了代码后发现是把RNN的最后一个预测值与$\tau$一起输入到FNN中了。中间这些层的权重都是正的,而且激活函数是$tanh$,最后一层的激活函数是$softplus$,即$\log{(1 + \exp(\cdot))}$。
预测下一个事件的发生时间的方式是:给定过去事件${t_1, t_2, \dots t_i}$,下一个事件的发生时间$t_{i+1}$的条件密度函数$p^\ast(t \mid t_1, t_2, \dots, t_i)$通过公式2计算。
\tag{2} p(t_{i+1} \mid t_1, t_2, \dots, t_i) = \lambda(t_{i+1} \mid H_{t_{i+1}}) \exp{{- \int^{t_{i+1}}_{t_i} \lambda(t \mid H_t) dt }}
这里使用预测分布$p^\ast$的中位数$t^\ast_{i+1}$来预测$t_{i+1}$。这里利用$\Phi(t^\ast_{i+1} - t_i \mid h_i) = \log{(2)}$这个关系来计算中位数$t^\ast_{i+1}$。这个关系通过在$[t_i, t_{i+1})$上面对强度函数积分得到,此时指数分布的均值为1,还可以对公式2直接积分得到。中位数$t^\ast_{i+1}$可以使用root finding方法,比如二分方法直接获得。本文的模型只需要1s就可以给20000个事件生成预测结果。因此累积hazard函数在生成中位数的预测中也很重要。