AAAI 2017, Intensity RNN: Modeling The Intensity Function Of Point Process Via Recurrent Neural Networks。相比RMTPP,用LSTM。然后模型加了一个时间序列模块,主要是为了支持有时间序列信息的数据集。然后计算事件发生时间的损失时,用了一个高斯核函数。本质上还是MSE,没啥区别。
1 Introduction
${z_i, t_i }^N_{i=1}$表示事件数据。事件序列的时间间隔不像时间序列那样相等。点过程是研究事件序列的重要方法。
最近一些机器学习方法在数学公式和优化技术上做了一些巧妙的修改,还有一些新的条件强度函数建模方法,主要是用一些数据集上的先验知识来刻画数据的性质。点过程的主要缺点是表达能力受限,模型太弱了,难以捕获复杂的数据。而且如果模型选错了的话,效果会很差。
本文将点过程的条件强度看作是模型的输入信息到事件发生强度之间的非线性映射。输入i西南西包含事件的类型、事件信息、系统历史。这样的非线性映射目标是足够复杂且足够灵活,可以对事件数据的特性建模。
本文用RNN编码这种非线性关系,在不用先验知识的情况下以端到端的形式建模非线性强度映射。
3 Network Structure and End-to-End Learning
RNN的输入序列${\mathbf{x}}^T_{t=1}$,隐藏状态${\mathbf{h}}^T_{t=1}$。本文用LSTM。
$$ \begin{align} \mathbf{i}\_t &= \sigma(\mathbf{W}\_i \mathbf{x}\_t + \mathbf{U}\_i \mathbf{h}\_{t-1} + \mathbf{V}\_i \mathbf{c}\_{t-1} + \mathbf{b}\_i),\\ \mathbf{f}\_t &= \sigma(\mathbf{W}\_f \mathbf{x}\_t + \mathbf{U}\_f \mathbf{h}\_{t-1} + \mathbf{V}\_f \mathbf{c}\_{t-1} + \mathbf{b}\_f),\\ \mathbf{c}\_t &= \mathbf{f}\_t \mathbf{c}\_{t-1} + \mathbf{i}\_t \odot \text{tanh}(\mathbf{W}\_c \mathbf{x}\_t + \mathbf{U}\_c \mathbf{h}\_{t-1} + \mathbf{b}\_c),\\ \mathbf{o}\_t &= \sigma(\mathbf{W}\_o \mathbf{x}\_t + \mathbf{U}\_o \mathbf{h}\_{t-1} + \mathbf{V}\_o \mathbf{c}\_t + \mathbf{b}\_o),\\ \mathbf{h}\_t &= \mathbf{o}\_t \odot \text{tanh}(\mathbf{c}\_t) \end{align} $$$\odot$表示element-wise multiplication,$\sigma$是sigmoid。
上述LSTM可以写为:
$$ (\mathbf{h}\_t, \mathbf{c}\_t) = \text{LSTM}(\mathbf{x}\_t, \mathbf{h}\_{t-1} + \mathbf{c}\_{t-1}) $$考虑两类输入:
- 连续等间隔分布的时间序列
- 间隔随机的事件数据
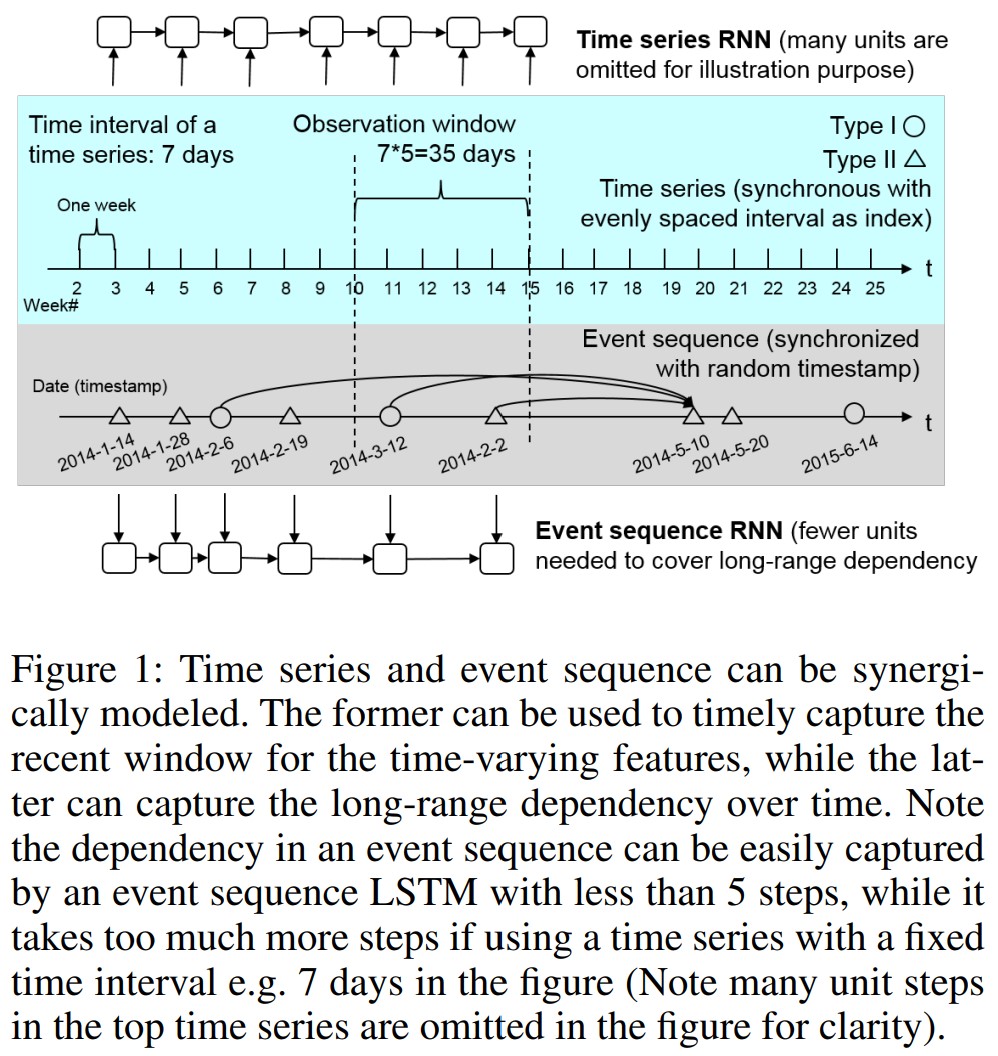
网络由两部分组成,一个RNN建模时间序列${y_t}^T_{t=1}$,捕获事件发生的background intensity,另一个建模事件序列${z_i, t_i}^N_{i=1}$,捕获long-range事件的依赖关系。因此:
$$ \begin{align} (\mathbf{h}^y\_t, \mathbf{c}^y\_t) &= \text{LSTM}\_y(\mathbf{y}\_t, \mathbf{h}^y\_{t-1} + \mathbf{c}^y\_{t-1}),\\ (\mathbf{h}^z\_t, \mathbf{c}^z\_t) &= \text{LSTM}\_z(\mathbf{z}\_t, \mathbf{h}^z\_{t-1} + \mathbf{c}^z\_{t-1}),\\ \mathbf{e}\_t &= \text{tanh}(\mathbf{W}\_f [\mathbf{h}^y\_t, \mathbf{h}^z\_t] + \mathbf{b}\_f),\\ \mathbf{U}\_t &= \text{softMax}(\mathbf{W}\_U \mathbf{e}\_t + \mathbf{b}\_U),\\ \mathbf{u}\_t &= \text{softMax}(\mathbf{W}\_u[\mathbf{e}\_t, \mathbf{U}\_t] + \mathbf{b}\_u),\\ s\_t &= \mathbf{W}\_s \mathbf{e}\_t + b\_s,\\ \end{align} $$$U$和$u$分别表示事件的主要类型和子类,$s$表示事件的时间戳,损失定义为:
$$ \sum^N\_{j=1}(- W^j\_U \log(U^j\_t) - w^j\_u \log(u^j\_t) - \log(f(s^j\_t \mid h^j\_{t-1}))) $$$N$是样本数,$j$是样本的index,$s^j_t$是下一个事件的时间戳,$h^j_{t-1}$是历史信息。第三项的含义是,我们不仅要预测对下一个事件的类型,也要让下一个事件的预测发生时间尽可能准确。这里用一个高斯惩罚函数,$\sigma^2 = 10$:
$$ f(s^j\_t \mid h^j\_{t-1}) = \frac{1}{\sqrt{2 \pi \sigma}} \exp(\frac{-(s^j\_t - \tilde{s}^j\_t)^2}{2\sigma^2}) $$时间戳预测层的输出$\tilde{s}^j_t$计算损失的时候,要计算上面的惩罚。
$W, w$分别是主类和子类的权重,用来平衡样本。这里说,如果主类和子类的预测是相互独立的,那么就把这两个数设为0。这里明显不对吧,设为0了损失不久只剩下事件发生时间了吗。。。。。。
用RMSprop优化。