IEEE Signal Processing Magazine 2013, 原文链接:The Emerging Field of Signal Processing on Graphs: Extending High-Dimensional Data Analysis to Networks and Other Irregular Domains
Abstract
社交、能源、运输、传感器、神经网络、高维数据很多都很自然地依赖于带权图的顶点。新兴的图信号处理领域融合了代数、谱图理论与计算谐波分析来处理图上的信号。在这篇教程中,我们列出了这个领域的主要挑战,讨论了定义图谱域的不同方法,点明了融合图数据域中不规则的结构在处理图信号时的重要性。然后回顾了将基础的操作,如filtering, translation, modulation, dilation, downsampling等技术泛化到图上的方法,对已经提出的高效地从图中的高维数据提取信息的localized, multisacle transforms进行了总结。最后对一些问题以及未来的扩展做了一些讨论。
1. Introduction
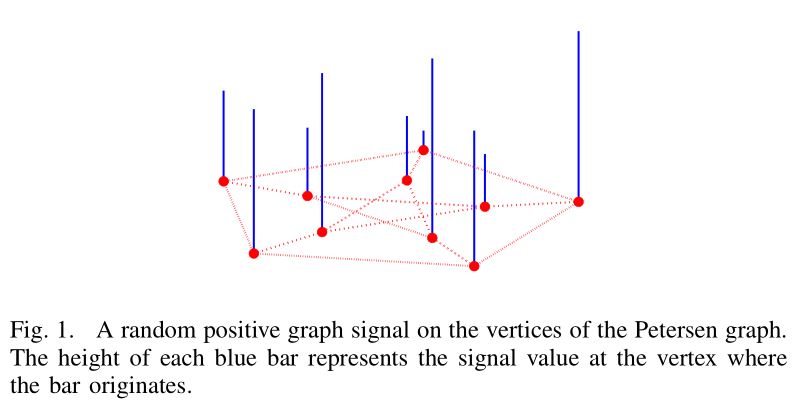
图是很多数据的表示形式,在描述很多应用的几何结构时很有用,如社交、能源、运输、传感器、神经网络等。图中每条边的权重,经常表示为两个顶点之间的相似度。连接性和边权重要么由问题的物理性质指明,要么从数据中推断出来。举个例子,边权重可能与网络中两个顶点之间的距离成反比。这些图的数据可以看作是一个样本的有限集合,每个顶点一个样本。我们称这些样本为一个图信号。一个图信号的例子如图1所示。
在运输网络中,我们关心分析描述疾病传播的传染病数据,描述用户迁移的人口数据,或是描述货物仓库的后勤数据。现在,在大脑图像中,推断大脑皮层上独特的功能区结构上的连接性变为可能,这种连接可以表示为一个带权图,顶点代表了功能区。因此,noisy fMRI图像可以看作是带权图上的信号。带权图一般用来表示统计学习问题中数据点之间的相似性,如计算机视觉和文本分类问题。事实上,很多研究图数据分析的论文是从统计学习社区中发表出来的,因为基于图的方法在半监督学习问题中变得非常流行,这些问题的目标是用一些标记样本对未知的样本进行分类。在图像处理,对图像的像素构造非局部和半局部连接的图的这种,基于图的filtering methods突然流行了起来,这些方法不仅基于像素间的物理相似性,还有要处理的图像的nosiy versions。这些方法经常能更好地识别并考虑图像的边和材质。
这些应用中常见的数据处理任务有filtering, denoising, inpainting, compressing graph signals。如何在不规则的域中处理他们,比如在任意结构的图上面?对数据的存储,通信,分析最有效的从高维数据中提取信息的方法是什么,统计与可视化?传统的信号处理的操作或算法可以使用吗?在图上的信号处理领域还有一些这样的问题。
A. The Main Challenges of Signal Processing on Graphs
小波,时频,曲波和其他局部变化来稀疏地表示不同类别的高维数据,如欧氏空间中的音频和图像信号,这种表示能力在之前提到的信号处理任务中取得了很多的成功。
$N$个顶点的图信号和一个传统的$N$个样本的离散时域信号可以看作是$\mathbb{R}^N$中的向量。然而,传统信号处理方法应用到图数据上的一个主要障碍是用离散时域信号的处理方式处理图信号时忽略了不规整的数据域内的关键依赖。此外,传统信号处理技术中的很多很简单的基础概念在图信号中变得很有挑战性: ·为了让一个模拟信号$f(t)$向右移动3,我们只要简单的改变变量,考虑$f(t-3)$即可。然而,把一个图信号向右移动3的意义就不是很清晰了。改变变量的方法不会有效因为$f(\circ - 3)$没有意义。一个朴素的方法是将顶点从$1$标到$N$,定义$f(\circ - 3) := f(\mathrm{mod}(\circ - 3, N))$,但是如果这个变换依赖于顶点的顺序的话,这个方法就不是很有用了。不可避免的是,带权图是不规则的结构,这种结构缺少一种变换的平移不变性的性质。 ·通过乘以一个复杂的指数项在实数线上对信号建模对应了傅里叶域中的变换。然而,图问题中的模拟谱是离散且不规则的,因此没有好的方法定义一种对应图谱域中的变换。 ·举个例子,我们凭直觉每隔一个数据点删除一个数据点,对离散时域信号做下采样。但是在图1中的图信号中这意味着什么?带权图中的“每隔一个顶点”没有明确的含义。 ·甚至我们做一个固定的下采样,为了在图上做一个多分辨率,我们需要一个生成粗糙版本的图的方法,这个方法可以捕获原始图中嵌入的结构属性。
此外,处理数据域的不规则性,图结构在之前提到的应用中,可以表示很多顶点的特征。为了能很好地对数据的尺度进行缩放,对于图信号的处理技术应该使用局部操作,通过对每个顶点,计算顶点的邻居,或是和它很近的顶点的信息得到。
因此,图信号处理的主要挑战是:1. 有些任务中图没有直接给出,需要决定如何构建可以捕获数据几何结构的带权图;2. 将图结构整合到局部变换操作中;3. 同时利用这些年来信号处理在欧氏空间发展出的理论成果;4. 研究局部变换的高效实现,从高维的图结构数据或其他不规则数据域中提取信息。
为了解决这些问题,新兴的图信号处理领域将代数和谱图理论的概念与计算谐波分析融合了起来。这是在代数图理论和谱图理论中的扩展;但是,早于十年前的研究主要是聚焦于分析图,而不是分析图的信号。
2. The Graph Spectral Domains
谱图理论是聚焦于构建、分析、操作图的,不是图上的信号。在构建扩展图、图的可视化、谱聚类、着色问题、还有许多如化学、物理、计算科学领域的问题上都很有效。
图信号处理领域,谱图理论被用作一个定义频谱和图傅里叶变换的基的扩展的工具。这部分我们会回顾一些谱图理论基本的定义与符号,研究它如何使得从传统的傅里叶分析扩展出很多重要的数学理论到图论上。
A. Weighted Graphs and Graph Signals
我们分析无向、连通图$\mathcal{G} = \lbrace \mathcal{V}, \mathcal{E}, \mathbf{W} \rbrace$上的信号。边$e = (i, j)$连接了顶点$i$和$j$,$W_{i,j}$表示边的权重,否则$w_{i,j} = 0$。如果$\mathcal{G}$有$M$个连通分量,我们可以将信号分为$M$份,然后将每份看作是一个子图进行处理。
当边的权重没有给出的时候,一种常用的方法是使用一个带阈值的高斯核权重函数:
$$\tag{1} W\_{i,j} = \begin{cases} \exp{(-\frac{[dist(i,j)]^2}{2\theta^2})} \quad &\text{if } dist(i, j) \leq \kappa \\ 0 \quad &\text{otherwise} \end{cases}, $$参数是$\theta$和$\kappa$。式1中,$dist(i, j)$表示顶点$i$和$j$之间的物理距离,或是两个顶点的特征向量的欧氏空间中的距离,后者在半监督学习任务中很常用。另一个常用的方法是基于物理距离或特征空间距离,将顶点与它的$k$最近邻顶点相连。其他构建图的方法,见第四章,14。
一个定义在图的顶点上的信号或函数$f: \mathcal{V} \rightarrow \mathbb{R}$可能表示成一个向量$\mathbf{f} \in \mathbb{R}^N$,第$i$个分量表示顶点集$\mathcal{V}$中的第$i$个顶点。
B. The Non-Normalized Graph Laplacian 非归一化的拉普拉斯矩阵,也称为组合拉普拉斯矩阵(combinatorial graph Laplacian),定义为$\bf L := D - W$,$\bf{D}$是对角矩阵,对角线上的第$i$个元素等于与顶点$i$相关的边的权重之和。拉普拉斯矩阵是一个差操作,因为对于任意一个信号$\mathbf{f} \in \mathbb{R}^N$,它满足:
$$ (\mathbf{L}f)(i) = \sum\_{j \in \mathcal{N}\_i} W\_{i,j}[f(i) - f(j)], $$邻居$\mathcal{N}_i$是与顶点$i$通过一条边相连的顶点集合。我们用$\mathcal{N}(i, k)$表示通过$k$步或小于$k$步连接到顶点$i$的顶点集合。 因为图的拉普拉斯矩阵$L$是实对称矩阵,它的特征向量相互正交,我们表示为$\lbrace \mathbf{u}_l \rbrace_{l=0,1,…,N-1}$。这些特征向量对应非负的特征值$\lbrace \lambda_l\rbrace_{l=0,1,…,N-1}$,满足$L \mathbf{u}_l = \lambda_l \mathbf{u}_l$,$l = 0,1,…,N-1$。零作为特征值,其多重性等于图的连通分量数,因为我们考虑的是连通图,我们假设拉普拉斯矩阵的特征值的顺序为:$0 = \lambda_0 < \lambda_1 \leq \lambda_2 … \leq \lambda_{N-1} := \lambda_{\text{max}}$。我们将整个谱表示为$\sigma(L) = \lbrace \lambda_0, \lambda_1, …, \lambda_{N-1}\rbrace$。
C. A Graph Fourier Transform and Notion of Frequency 传统的傅里叶变换
$$ \hat{f}(\xi) := \langle f, e^{2\pi i \xi t} \rangle = \int\_\mathbb{R} f(t) e^{-2\pi i \xi t}dt $$是函数$f$根据复指数的扩展,是一维拉普拉斯算子的特征函数:
$$\tag{2} -\Delta(e^{2\pi i \xi t}) = -\frac{\partial^2}{\partial t^2} e^{2\pi i \xi t} = (2 \pi \xi)^2 e^{2\pi i \xi t}. $$类比这个,我们可以定义任何一个在图$\mathcal{G}$的顶点上的函数$\mathbf{f} \in \mathbb{R}^N$的图傅里叶变换$\hat{\mathbf{f}}$,根据图拉普拉斯矩阵的特征向量对$\mathbf{f}$的扩展:
$$\tag{3} \hat{f}(\lambda\_l) := \langle \mathbf{f}, \mathbf{u}\_l \rangle = \sum^N\_{i = 1} f(i) u^*\_l (i). $$逆图傅里叶变换为:
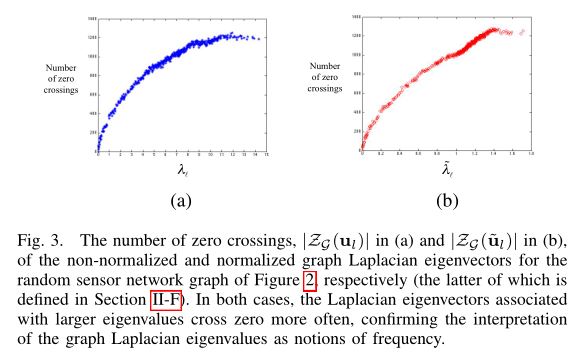
$$\tag{4} f(i) = \sum^{N - 1}\_{l = 0} \hat{f}(\lambda\_l) u\_l(i). $$传统的傅里叶分析中,式2中的特征值$\lbrace (2 \pi \xi )^2 \rbrace_{\xi \in \mathbb{R}}$对频率有特殊性:对于$\xi$接近0(低频),对应的复指数特征函数是平滑的,震荡慢的函数,而$\xi$远离0(高频)的对应的复指数特征函数震荡的很快。在图任务中,图拉普拉斯矩阵的特征值和特征向量在频率上提供了相似的特点。对于连通图,拉普拉斯矩阵的对应特征值为0的特征向量$\mathbf{u}_0$是不变的,且每个顶点的值为$\frac{1}{\sqrt{N}}$。图拉普拉斯矩阵的特征向量中对应低频的$\lambda_l$在图上变化的慢;也就是,如果两个顶点通过一条权重很大的边连接,这些地方的特征向量的值就会变得比较相似。对应大的特征值的特征向量在图上变化的更快,且边的权重越高,这些顶点上的值越不相似。图2给出了不同的随机的sensor网络的拉普拉斯矩阵的特征向量,图3展示了每个特征向量zero crossing的数量$\vert Z_\mathcal{G}(\cdot) \vert$。一个信号$\bf{f}$在图$\mathcal{G}$的zero crossing的集合定义为:
$$ Z\_\mathcal{G}(\mathbf{f}) := \lbrace e = (i, j) \in \Large\varepsilon \normalsize : f(i)f(j) < 0 \rbrace; $$也就是,连接一个正信号和一个负信号的边的集合。
D. Graph Signal Representations in Two Domains
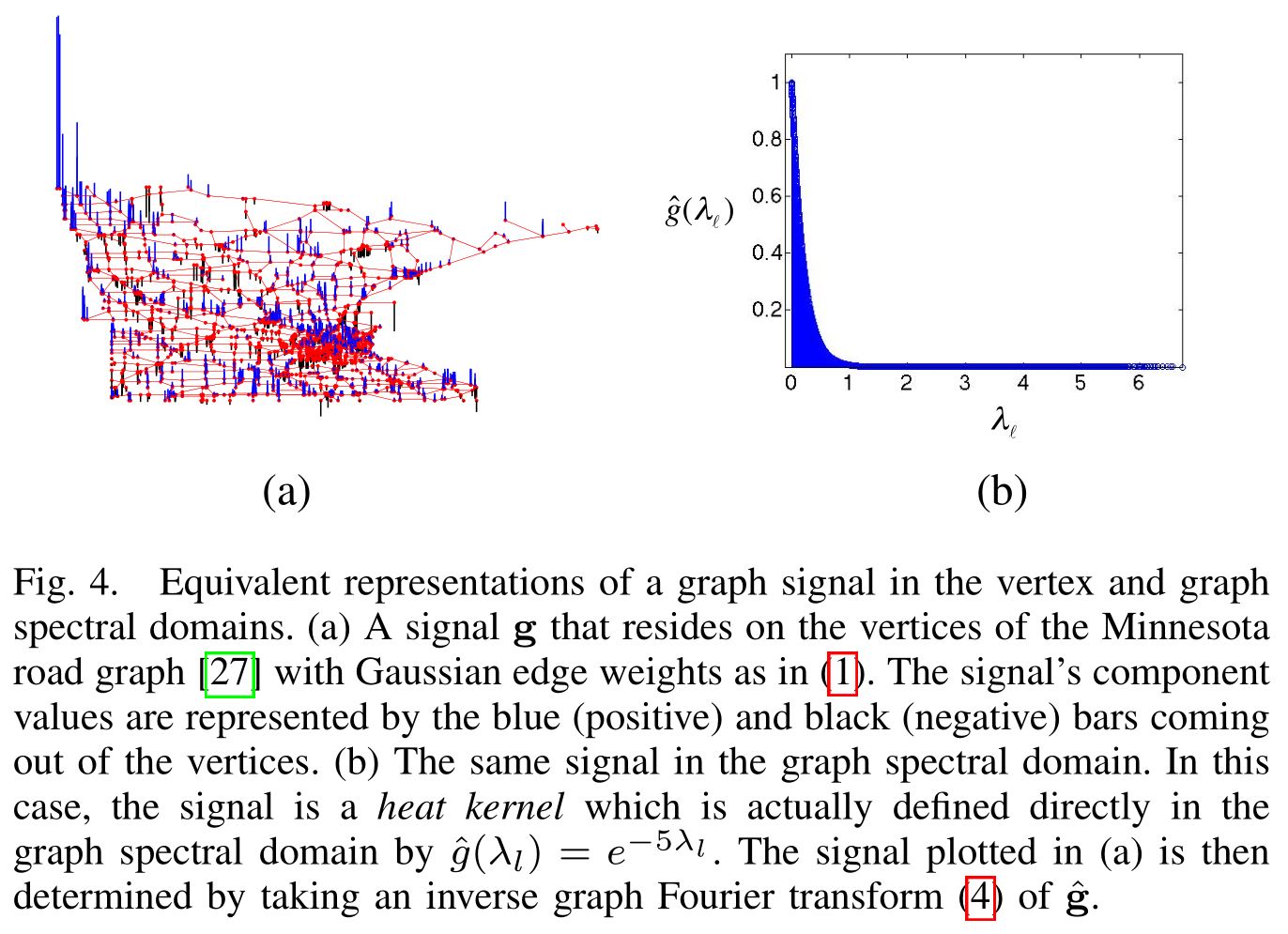
图傅里叶变换(3)和它的逆(4)给了我们一种方式在两个不同的域中等价的表示一个信号:顶点域和图谱域。尽管我们经常从顶点域的一个信号$\bf{g}$开始,直接在图谱域中定义一个信号$\hat{\bf{g}}$可能仍然是有用的。我们称这样的信号为核(kernels)。图4a和图4b中,一个这样的核,一个heat kernel,分别展示了在两个域中的效果。类比传统的模拟情况,图4中展示的一个平缓的信号图傅里叶系数衰减的很快。这样的信号是可压缩的(compressible),因为可以通过调整一些图傅里叶系数来趋近他们。
E. Discrete Calculus and Signal Smoothness with Respect to the Intrinsic Structure of the Graph
分析信号时,需要强调一点是,属性(如smoothness)与数据域的内在结构相对应,在我们讨论的环境中,就是带权图。尽管微分几何提供了方法将潜在流形的几何结构整合进可微分流形上连续信号的分析中,*离散微积分(discrete calculus)*提供了一组可以在有限离散空间中操作的多变量微积分的定义与可微分操作器。
为了增加smoothness对应图的内在结构的问题,我们简单的提一些离散可微分操作。一个信号$\bf{f}$在顶点$i$,对于边$e = (i, j)$的边导数(edge derivative)定义为:
$$ \left. \frac{\partial \mathbf{f}}{\partial e} \right|\_i := \sqrt{W\_{i,j}}[f(j) - f(i)], $$顶点$i$处$\bf{f}$的图梯度是:
$$ \nabla\_i \mathbf{f} := [\lbrace \left. \frac{\partial f}{\partial b} \right|\_i \rbrace\_{e \in \varepsilon \ \text{s.t.} \ e=(i,j) \ \text{for some} \ j \in \mathcal{V}}]. $$顶点$i$的local variation
$$ \begin{aligned} \Vert \nabla\_i \mathbf{f} \Vert\_2 : & = [\sum\_{e \in \varepsilon \ \text{s.t.} \ e =(i, j) \ \text{for some} \ j \in \mathcal{V}} (\left. \frac{\partial \mathbf{f}}{\partial e} \right|\_i)^2]^{\frac{1}{2}} \\ & = [\sum\_{j \in \mathcal{N}\_i} W\_{i, j} [f(j) - f(i)]^2]^{\frac{1}{2}} \end{aligned} $$可以度量顶点$i$周围的$\bf{f}$的local smootheness,当顶点$i$和它的邻居$j$的$\bf{f}$有相近的值时这个值较小。
对于global smoothness,$\bf{f}$的discrete p-Dirichlet form定义为:
$$\tag{5} S\_p(\mathbf{f}) := \frac{1}{p} \sum\_{i \in V} \Vert \nabla\_i \mathbf{f} \Vert^p\_2 = \frac{1}{p} \sum\_{i \in V}\LARGE[ \normalsize \sum\_{j \in \mathcal{N}\_i} W\_{i,j} [f(j) - f(i)]^2 \LARGE]^{\normalsize \frac{p}{2}}. $$当$p=1$时,$S_1(\mathbf{f})$是信号对图的total variation。当$p = 2$时:
$$\tag{6} \begin{aligned} S\_2(\mathbf{f}) &= \frac{1}{2}\sum\_{i \in V} \sum\_{j \in \mathcal{N}\_i} W\_{i,j} [f(j) - f(i)]^2 \\ &= \sum\_{(i,j) \in \varepsilon} W\_{i,j} [f(j) - f(i)]^2 = \mathbf{f^TLf}. \end{aligned} $$$S_2(\mathbf{f})$被称为图拉普拉斯矩阵的二次型,semi-norm $\bf \Vert f \Vert_L$定义为:
$$ \Vert \mathbf{f} \Vert\_\mathbf{L} := \Vert \mathbf{L}^{\frac{1}{2}} \mathbf{f} \Vert\_2 = \sqrt{\mathbf{f^TLf}} = \sqrt{S\_2(\mathbf{f})}. $$注意式6,二次型$S_2(\mathbf{f})$等于0当且仅当$\bf{f}$在所有顶点上都为常数(which is why $\Vert \mathbf{f} \Vert_L$ is only a semi-form),而且,更一般地,当信号$\bf{f}$在那些通过大权重的边连接的邻居顶点上有相似值时,$S_2(\mathbf{f})$的值较小;也就是当它平滑的时候。
回到拉普拉斯矩阵的特征值和特征向量上,Courant-Fischer Theorem指出,他们也可以通过Rayleigh quotient定义为:
$$\tag{7} \lambda\_0 = \min\_{ \mathbf{f} \in \mathbb{R}^N, \Vert \mathbf{f} \Vert\_2 = 1} \lbrace \mathbf{f^TLf} \rbrace, $$$$\tag{8} \text{and} \ \lambda\_l = \min\_{ \mathbf{f} \in \mathbb{R}^N, \Vert \mathbf{f} \Vert\_2 = 1, \mathbf{f} \perp span\lbrace \mathbf{u}\_0, ..., \mathbf{u}\_{l-1} \rbrace} \lbrace \mathbf{f^TLf} \rbrace, \ l = 1, 2, ..., N-1. $$其中,特征向量$\mathbf{u}_l$是第$l$个问题的最小化问题的解。从式6和式7中,我们可以再次看出为什么$\mathbf{u}_0$对于连通图来说是常数。式8解释了为什么拉普拉斯矩阵中对应小的特征值的特征向量更平滑,也提供了另一个对为什么拉普拉斯矩阵的谱反映了频率的解释。
总结一下,图的连通性编码进了拉普拉斯矩阵,拉普拉斯矩阵通常用于定义图傅里叶变换(通过特征向量),平滑性的不同表示。Example 1展示了smoothness和一个图信号的谱内容是如何依赖于图的。
F. Other Graph Matrices 图拉普拉斯矩阵的基$\lbrace \mathbf{u}_l \rbrace_{l = 0, 1, …, N - 1}$只是在正向(3)和逆向(4)图傅里叶变换中使用的一组可能的基。第二个常用的normalize每个权重$W_{i,j}$的方法是乘以$\frac{1}{\sqrt{d_i d_j}}$。这样可以对图的拉普拉斯矩阵归一化,定义为$\bf\tilde{L} := D^{-\frac{1}{2}} L D^{-\frac{1}{2}}$,等价于:
$$ (\tilde{L}f)(i) = \frac{1}{\sqrt{d\_i}} \sum\_{j \in \mathcal{N}\_i} W\_{i,j} \LARGE[\normalsize \frac{f(i)}{\sqrt{d\_i}} - \frac{f(j)}{\sqrt{d\_j}} \LARGE]. $$连通图$\mathcal{G}$的归一化的拉普拉斯矩阵的特征值$\lbrace \tilde{\lambda}_l \rbrace_{l=0,1,…,N-1}$满足:
$$ 0 = \tilde{\lambda}\_0 < \tilde{\lambda}\_1 \leq ... \leq \tilde{\lambda}\_{\text{max}} \leq 2, $$当且仅当$\mathcal{G}$是二分图时,$\tilde{\lambda}_{\text{max}} = 2$。我们将归一化的拉普拉斯矩阵表示为$\lbrace \mathbf{\tilde{u}}_l \rbrace_{l = 0,1,…N-1}$。图3b中,$\tilde{L}$的谱和频率也有关系,对应大的特征值的特征向量一般有着更多的zero crossing。然而,不像$\mathbf{u}_0$,归一化的拉普拉斯矩阵中对应特征值为0的$\tilde{\mathbf{u}}_0$不是一个常向量。
归一化和非归一化的拉普拉斯矩阵都是generalized graph Laplacians的例子,也称为discrete Schrödinger operators。一个图$\mathcal{G}$的泛化拉普拉斯矩阵是任意的对阵矩阵,如果这个矩阵中有边连接顶点$i$和顶点$j$,那么这个矩阵的$(i, j)$是负的,如果$i \not = j$,而且$i$与$j$不相连,那么为$0$,如果$i = j$,那么有可能是任何值。
第三个常用的矩阵,经常在图信号的降维技术中使用,是random walk matrix,$\bf{P := D^{-1}W}$。每个值$P_{i,j}$表示在图$\mathcal{G}$上从顶点$i$到顶点$j$通过一步马尔可夫随机游走的概率。对于连通的、非周期的图,$\mathbf{P}^t$在$t$趋近于无穷时,收敛至平稳分布。与随机游走矩阵密切相关的是非对称拉普拉斯矩阵,定义为 $\mathbf{L}_a := \mathbf{I}_N - \mathbf{P}$,其中$\mathbf{I}_N$表示$N \times N$的单位阵。注意$\mathbf{L}_a$有着和$\tilde{\mathbf{L}}$同样的特征值集合,如果$\tilde{\mathbf{u}}_l$是对应$\tilde{L}$的特征值$\tilde{\lambda}_l$的特征向量,则$\bf{D}^{-\frac{1}{2}} \tilde{\mathbf{u}}_l$是对应$\mathbf{L}_a$的特征值$\tilde{\lambda}_l$的特征向量。
正如下一节要讨论的,归一化和非归一化的拉普拉斯矩阵都能用于filtering。没有明确的规定要求什么时候必须使用归一化的,什么时候使用非归一化的拉普拉斯矩阵的特征向量,什么时候使用其他的基。归一化的拉普拉斯矩阵有很好的性质,它的谱总时在$[0, 2]$区间内,而且对于二分图,spectral folding phenomenon可以研究。然而,非归一化的拉普拉斯矩阵中对应特征值为0的特征向量是常向量,这在从传统filtering理论扩展关于信号的DC components上是一个有用的性质。
3. Generalized Operators For Signals on Graphs
在这部分,我们会回顾不同的方式来泛化基本操作到图上,如filtering, translation, modulation, dilation, downsampling。这些泛化的操作是第四部分要讨论的localized, multiscale transforms的基础。
A. Filtering 第一个泛化的操作是filtering。我们从扩展频率滤波的概念到图上开始,然后讨论顶点域上的局部滤波。
1. Frequency Filtering:
在传统的信号处理中,频率滤波是将输入信号表示成一个复指数的线性组合,扩大或缩小一些复指数贡献的过程
$$\tag{9} \hat{f}\_{out}(\xi) = \hat{f}\_{in}(\xi) \hat{h}(\xi), $$其中,$\hat{h}(\cdot)$是滤波器的传递函数。取式9的逆傅里叶变换,傅里叶域中的乘法对应了时域中的卷积:
$$\tag{10} f\_{out}(t) = \int\_\mathbb{R} \hat{f}\_{in}(\xi) \hat{h}(\xi)e^{2 \pi i \xi t} d\xi $$$$\tag{11} =\intop\_\mathbb{R} f\_{in}(\tau) h(t-\tau)d\tau =: (f\_in * h)(t). $$一旦我们fix一个图谱表示,我们的图傅里叶变换的概念,我们可以直接将式9泛化到定义频率滤波上,或图谱滤波(graph spectral filtering)上:
$$\tag{12} \hat{f}\_{out}(\lambda\_l) = \hat{f}\_{in}(\lambda\_l) \hat{h}(\lambda\_l), $$或者,等价的,取逆图傅里叶变换,
$$\tag{13} f\_{out}(i) = \sum^{N-1}\_{l=0} \hat{f}\_{in}(\lambda\_l) \hat{h}(\lambda\_l) u\_l(i). $$接用matrix functions[38]理论中的符号,我们可以将式12和式13写成$\mathbf{f}_{out} = \hat{h}(\mathbf{L})\mathbf{f}_{in}$,其中
$$\tag{14} \hat{h}(\mathbf{L}) := \mathbf{U} \begin{bmatrix} \hat{h}(\lambda\_0) & & 0 \\ & \ddots & \\ 0 & &\hat{h}(\lambda\_{N-1}) \end{bmatrix}\mathbf{U^T} $$基础的图谱滤波可以用来实现连续滤波技术的离散版,如高斯平滑,双边滤波,total variation filtering,anisotropic diffusion,non-local means filtering。特别地,这些滤波器中的很多成为了解决variational problems的方法,对ill-posed inverse problems进行正则化,这些问题如denoising,inpainting,super-resolution。举个例子,离散正则框架:
$$\tag{15} \min\_\mathbf{f}\lbrace \Vert \mathbf{f} - \mathbf{y} \Vert^2\_2 + \gamma S\_p(\mathbf{f}) \rbrace, $$其中,$S_p(\mathbf{f})$是式5的p-Dirichlet form。在Example 2中,我们举了个式15的$p = 2$时处理图像去噪的问题的例子。
2. Filtering in the Vertex Domain:
在顶点域中filter一个信号,只要简单的将顶点$i$的输出$f_{out}(i)$写成一个顶点$i$的$K-hop$局部邻居上输入信号各分量的线性组合:
$$\tag{18} f\_{out}(i) = b\_{i, i} f\_{in}(i) + \sum\_{j \in \mathcal{N}(i, K)} b\_{i,j} f\_{in}(j), $$$\lbrace b_{i,j} \rbrace_{i,j \in \mathcal{V}}$是常数。式18只说明了顶点域上的滤波是一个局部的线性变换。
我们现在简单地将图谱域上的滤波关联到了顶点域的滤波上。当式12中的频率滤波是$K$阶多项式$\hat{h}(\lambda_l) = \sum^K_{k=0} a_k \lambda^k_l$时,其中$\lbrace a_k\rbrace_{k=0,1,…K}$是常数,我们也可以将式12在顶点域中解释。由式13,我们得到:
$$\tag{19} \begin{aligned} f\_{out}(i) & = \sum^{N-1}\_{l=0} \hat{f}\_{in}(\lambda\_l) \hat{h}(\lambda\_l) u\_l(i) \\ & = \sum^N\_{j=1} f\_{in}(j) \sum^K\_{k=0} a\_k \sum^{N-1}\_{l=0} \lambda^k\_l u^*\_l(j) u\_l(i) \\ & = \sum^N\_{j=1} f\_{in}(j) \sum^K\_{k=0} a\_k(\mathbf{L}^k)\_{i,j}. \end{aligned} $$然而,在顶点$i$到顶点$j$之间的最短路径距离$d_\mathcal{G}(i,j)$大于$k$时,$(\mathbf{L}^k)_{i,j} = 0$。因此,我们可以将式19写成式18,常数定义为:
$$ b\_{i,j} := \sum^K\_{k=d\_\mathcal{G}(i,j)} a\_k (\mathbf{L}^k)\_{i,j}. $$所以当频率滤波是一个$K$阶多项式时,顶点$i$上频率滤波后的信号,$f_{out}(i)$,是顶点$i$的$K-hop$邻居上的输入信号的线性组合。这个性质在关联一个卷积核的平滑性与顶点域中滤波后信号的局部化之间很有用。
B. Convolution 我们不能直接将卷积的定义(11)泛化到图上,因为$h(t - \tau)$。然而,一种定义图上的卷积的方式是替换式10中的复指数为拉普拉斯矩阵的特征向量:
$$\tag{20} (f * h)(i) := \sum^{N-1}\_{l=0} \hat{f}(\lambda\_l) \hat{h}(\lambda\_l) u\_l(i), $$这个使得在顶点域上的卷积等价于在图谱域的乘法。
C. Translation