Multistep Speed Prediction on Traffic Networks: A Graph Convolutional Sequence-to-Sequence Learning Approach with Attention Mechanism

AGC-Seq2Seq，投的是TRC。清华大学和高德地图合作的一项研究。作者采用了 GCN + Seq2Seq + Attention 的混合模型，将路网中的边构建成图中的结点，在 GCN 上做了改进，将邻接矩阵扩展到 k 阶并与一个权重矩阵相乘，类似 HA-GCN(2016)，实现了邻居信息聚合时权重的自由调整，可以处理有向图。时间关系上使用 Seq2Seq + Attention 建模，完成了北京市二环线的多步的车速预测，对比的方法中没有近几年出现的时空预测模型。

摘要

为了在多步交通预测的任务中，捕获复杂的非平稳的时间动态性和空间依赖关系，我们提出了一个叫注意力图卷积序列到序列模型（AGC-Seq2Seq）。空间和时间用图卷积和序列到序列模型分开建模。注意力机制用来解决序列到序列模型在多步预测上的困难，同时来捕获交通流的异质性。

2. LITERATURE REVIEW

如 Li et al. 2017 所述，统计模型、shallow machine learning models 和 深度学习模型是三个主要的方法。

统计模型基于过去的时间序列观测值对未来进行预测。ARIMA 模型，Kalman filter，还有它们衍生出的算法。然而，简单的时间序列模型通常依赖平稳假设，这与城市交通的动态性不符。特别是对于多步时间预测，后面的预测值是基于前面的预测值的，因此，预测的误差会逐渐的传播。使用简单的时间序列预测模型很难满足高精度的预测需求。

同时，机器学习方法在交通预测研究中表现的很好。神经网络模型，贝叶斯网络，支持向量机模型，K 近邻摩西那个，随机森林模型在交通流预测中表现的很好。然而，机器学习算法的表现依赖于手工选取特征，而且选取特征的方法是不存在的，因为关键特征一般因问题而异。因此，使用元素级别的机器学习方法在复杂的预测任务上不会产生好的效果。

最近，深度学习算法成功的应用在计算机科学中，同时，它在运输学科也吸引了很多人的注意。Huang et al. 2014 使用深度置信网络用于无监督学习，证明了在交通流预测上的有效性。Lv et al. 2015 使用一个堆叠的自编码器模型学习交通流特征。Ma et al 2015 使用 LSTM 有效地捕获了交通流的动态性。Polson and Sokolov 2017 融合了 $L_1$ 正则和 $\text{tanh}$ 激活的多层网络来检测交通流的极端的非线性。然而，这些方法主要聚焦于对单个序列建模，不能反映交通网络的空间关系。

卷积神经网络提供了一个有效的架构来提取大尺度、高维的数据集中有效的统计模式。在学习局部平稳结构中，CNN 的能力在图像和视频识别任务中获得了很大的突破。在运输领域，也有学者使用 CNN 捕获交通网络上的空间关系。Ma et al. (2017) 提出了一个预测车速的深度卷积神经网络，将交通的时空动态性转换成图像。Wang et al. (2017) 将高速公路处理成一个 band image，提出了误差回传的循环卷积神经网络结构用于连续的交通速度预测。Ke et al. (2017) 将城市区域划分成均匀的网格，通过将卷积和 LSTM 层合并来预测每个网格内的乘客需求。上述的研究将交通网络转换为网格是因为 CNN 受限于处理欧氏空间的数据。然而，在交通预测上，路网上的时间序列是分布在一个拓扑图上连续的序列，是一种非欧式结构数据的典型 (Narang et al., 2013)；原本的 CNN 结构是不能使用的。为了解决这个问题，基于谱图理论的图卷积网络 (GCN) 可以用于在非欧式空间上使用卷积 (Kipf and Welling, 2016)。几个刚刚发表的研究在交通预测上使用了图卷积模型。基于谱的图卷积和时间上的卷积相结合 (Yu et al., 2017)，还有图卷积与循环神经网络 (RNN) 的结合 (Li et al., 2017) 来用于预测交通状态。之后，Cui et al. (2018) 使用高阶图卷积来学习路网上不同路段间的交互关系。上述研究没有在路网上直接定义图卷积，而是通过高斯核根据任意两个监测器间的距离构建了监测器之间的网络。此外，交通状况的时间关联也没有考虑。

总结一下，城市路网上交通状况的变化展示出了时空的依赖性。我们提出了一个定制版的深度学习框架，在 Seq2Seq 框架中继承了注意力机制和图卷积模型，同时捕获复杂的非平稳的空间动态性和多步交通预测的空间依赖性。

3. AGC-SEQ2SEQ DEEP LEARNING FRAMEWORK

3.1 Preliminaries

(1) Road network topology

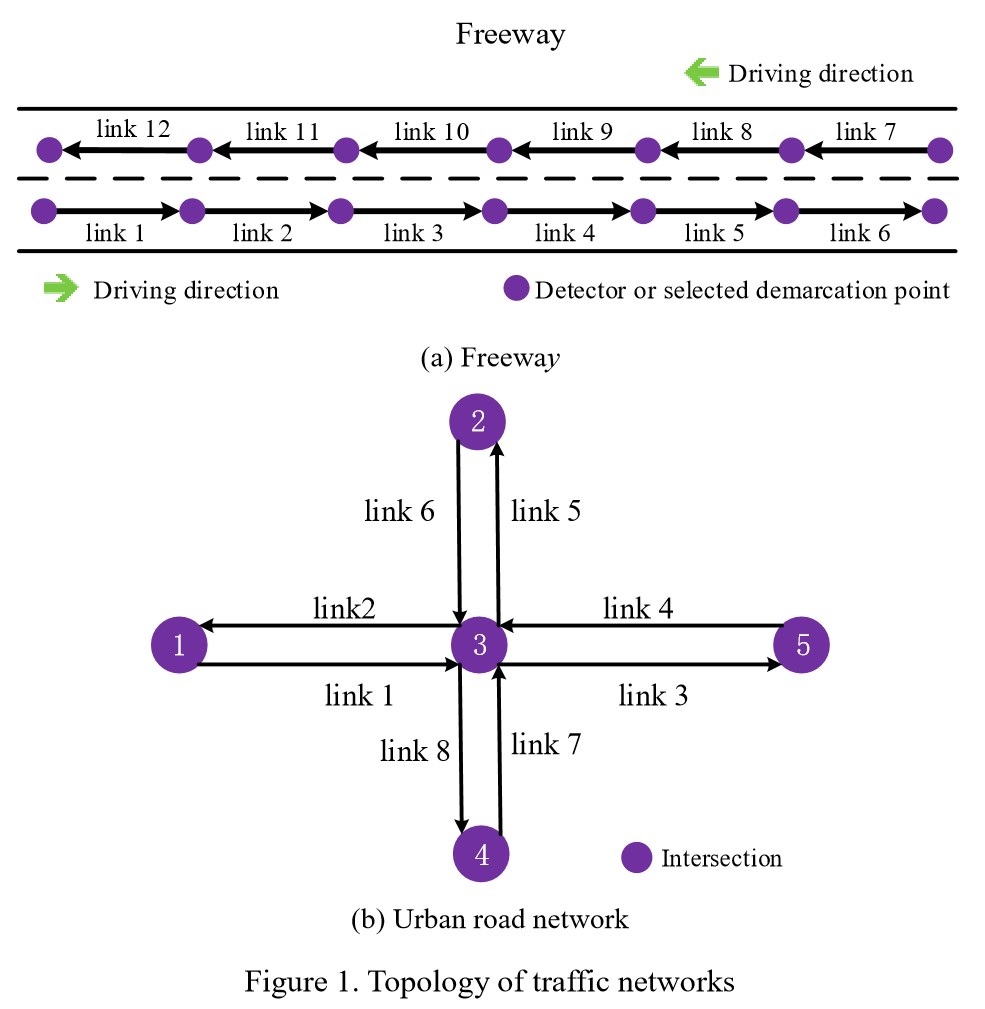
路网根据驾驶方向构建成有向图 $\mathcal{G}(\mathcal{N}, \mathcal{L})$ ，顶点集 $\mathcal{N}$ 表示路口 (监测器或选择的高速公路的划分点)，边集 $\mathcal{L}$ 表示路段，如图1所示。$\boldsymbol{A}$ 是边集的邻接矩阵，$\boldsymbol{A}(i, j)$ 表示边 $i$ 和 $j$ 是否相连，即

$$\boldsymbol{A}(i, j) = \begin{cases} 1, &\text{if } \quad l_i \quad \text{and} \quad l_j \quad \text{are} \quad \text{connected} \quad \text{along} \quad \text{driving} \quad \text{direction}\\ 0, &\text{if } \quad \text{otherwise} \end{cases}$$

(2) Traffic speed

路段 $l_i (\forall l_i \in \mathcal{L})$ 的第 $t$ 个时段（比如 5 分钟）定义为路段上这个时间段浮动车的平均速度，表示为 $v^i_t$。路网在第 $t$ 个时段的速度定义为向量 $\boldsymbol{V}_t \in \mathbb{R}^{\vert \mathcal{L} \vert}$（$\vert \mathcal{L} \vert$ 是边集 $\mathcal{L}$ 的基数），第 $i$ 个元素是 $(\boldsymbol{V}_t)_i = v^i_t$。

作为典型的时间序列预测问题，最近邻的 $m$ 步观测值可以对多步预测提供有价值的信息。除了实时的车速信息，一些外部变量，如时间、工作日还是周末，历史的统计信息也对预测有帮助。

(3) Time-of-day and weekday-or-weekend

因为路段的车速是聚合 5 分钟得到的平均值，时间会被转化为一个有序的实数，比如 00:00-00:05 转化为 $N_t = 1$，7:00-7:05 转化为 $N_t = 85(7 * 12 + 1)$，工作日或周末表示为 $p_t$，区分工作日和周末的不同特性。

(4) Historical statistic information

交通状态的每日趋势可以通过引入历史的统计数据捕获。历史的平均车速，中值车速，最大车速，最小车速，路段 $l_i$ 的 $t$ 时段的标准差，分别定义为训练集中的平均值、中位数、最大、最小、标准差，表示为 $v^i_{t,average}, v^i_{t,median}, v^i_{t,max}, v^i_{t,min}, d^i_t$。

(5) Problem formulation

车速预测是用之前观测到的速度预测一个确定时段每个路段上的车速。多步速度预测问题定义为：

$$\tag{1} \hat{V}_{t+n} = \mathop{\arg\max}\limits_{V_{t+n}} \text{Pr}(V_{t+n} \mid V_t, V_{t-1}, \dots, V_{t-m};\mathcal{G})$$

其中 $\hat{V}_{t+n}(n=1,2,3,\dots)$ 表示第 $n$ 步的预测速度，$\lbrace V_t, V_{t-1}, \dots, V_{t-m} \mid m=1,2,\dots \rbrace$ 是之前观测到的值。$\text{Pr}(·\mid·)$ 是条件概率。

3.2 Graph Convolution on Traffic Networks

图卷积通过谱域，将传统的卷积从网格上扩展到了图上。为了引入一般的 $K$ 阶图卷积，我们首先给每个路段 $l_i \in \mathcal{L}$ 定义了 $K$ 阶邻居 $\mathcal{H}_i(K) = \lbrace l_j \in \mathcal{L} \mid d(l_i, l_j) \leq K \rbrace$，其中 $d(l_i, l_j)$ 表示所有从 $l_i$ 到 $l_j$ 的路径中最短路径的长度。

邻接矩阵就是一阶邻居，$K$ 次幂就是 $K$ 阶邻居。为了模仿拉普拉斯矩阵，我们在对角线上加了1，定义为：

$$\tag{2} \boldsymbol{A}^K_{GC} = \text{Ci}(\boldsymbol{A}^K + \boldsymbol{I})$$

其中 $\text{Ci}(·)$ 是clip function，将非0元素变成1；因此 $\boldsymbol{A}^K_{GC}(i, j) = 1 \quad for \quad l_j \in \mathcal{H}_i(K) \quad or \quad i = j$；否则 $\boldsymbol{A}^K_{GC}(i, j) = 0$。单位阵 $\boldsymbol{I}$ 增加了自连接，卷积的时候可以考虑到自身。

基于上述的邻居矩阵，一个简单版本的图卷积(e.g., Cui et al., 2018)可以定义为：

$$\tag{3} \boldsymbol{V}_t(K) = (\boldsymbol{W}_{GC} \odot \boldsymbol{A}^K_{GC})\cdot \boldsymbol{V}_t$$

其中 $\boldsymbol{W}_{GC}$ 是一个和 $\boldsymbol{A}$ 一样大小的可训练的矩阵。$\odot$ 表示哈达玛积。通过哈达玛乘积，$(\boldsymbol{W}_{GC} \odot \boldsymbol{A}^K_{GC})$ 可以得到一个在 $K$ 阶邻居上有参数，其他地方为0的新矩阵。因此，$(\boldsymbol{W}_{GC} \odot \boldsymbol{A}^K_{GC})\cdot \boldsymbol{V}_t$ 可以理解成是一个对 $\boldsymbol{V}_t$ 的空间离散的卷积。结果就是，$\boldsymbol{V}_t(K)$ 是时间 $t$ 的融合空间的速度向量。它的第 $i$ 个元素 $v^i_t(K)$ 表示路段 $l_i \in \mathcal{L}$ 在时间 $t$ 的空间融合速度，这个速度集成了其邻居路段 $\mathcal{H}_i(K)$ 的信息。

此外，式3可以分解成一个一维卷积。

$$\tag{4} v^i_t(K) = (\boldsymbol{W}_{GC}[i] \odot \boldsymbol{A}^K_{GC}[i])^T \cdot \boldsymbol{V}_t$$

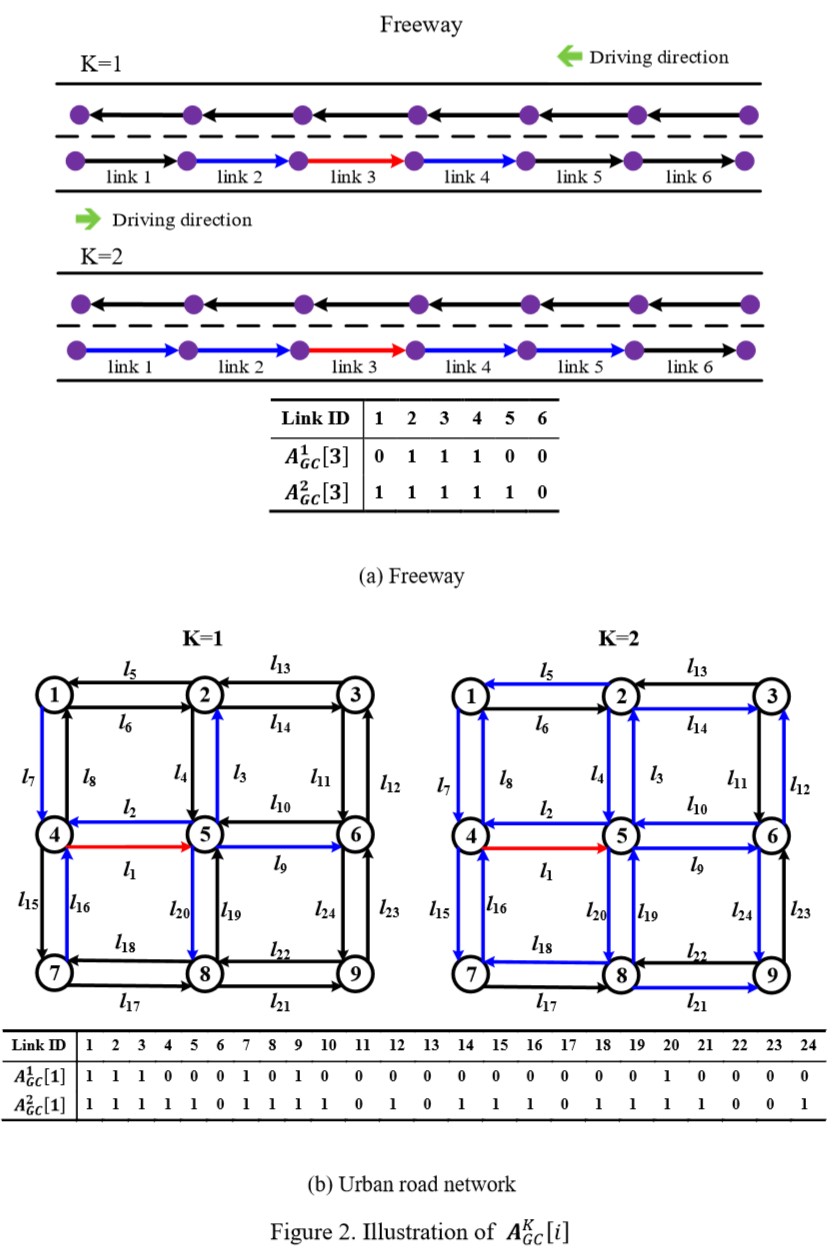
$\boldsymbol{W}_{GC}[i]$ 和 $\boldsymbol{A}^K_{GC}[i]$ 分别是 $\boldsymbol{W}_{GC}$ 和 $\boldsymbol{A}^K_{GC}$ 的第 $i$ 行。图2是路网上 $\boldsymbol{A}^K_{GC}[i]$ 的一个例子，路段 $i$ 在红线，邻居是蓝线。

3.3 Attention Graph Convolutional Sequence-to-Sequence Model (AGC-Seq2Seq)

我们提出了 AGC-Seq2Seq 模型将时空变量和外部信息集成至深度学习架构中，用来做多步车辆速度预测。

为了捕获时间序列特征和获得多步输出，我们使用 Seq2Seq 作为整个方法的基础结构，由两个参数独立的 RNN 模块组成(Sutskever et al., 2014; Cho et al., 2014)。为了克服 RNN 输出的长度不可变，Seq2Seq 模型将输入进编码器的时间序列编码，解码器从 context vector 中解码出预测值。我们提出的 AGC-Seq2Seq 模型如图3所示。首先用图卷积来捕获空间特征，然后将时空变量 $v^i_{t-j}(K)$ 和外部信息 $\boldsymbol{E}_{t-j}$（包括时间和工作日或周末信息）融合构成输入向量，然后放入 Seq2Seq的编码模型中。上述过程如下：

$$\tag{5} v^i_{t-j}(K) = (\boldsymbol{W}_{GC}[i] \odot \boldsymbol{A}^K_{GC}[i])^T \cdot \boldsymbol{V}_{t-j}, \quad 0 \leq j \leq m$$ $$\tag{6} \boldsymbol{E}_{t-j} = [N_{t-j};p_{t-j}]$$ $$\tag{7} \boldsymbol{X}^i_{t-j} = [v^i_{t-j}(K);\boldsymbol{E}_{t-j}]$$

其中 $N_{t-j}$ 和 $p_{t-j}$ 如3.1节定义，$[·;·]$ 操作是将两个张量拼接。

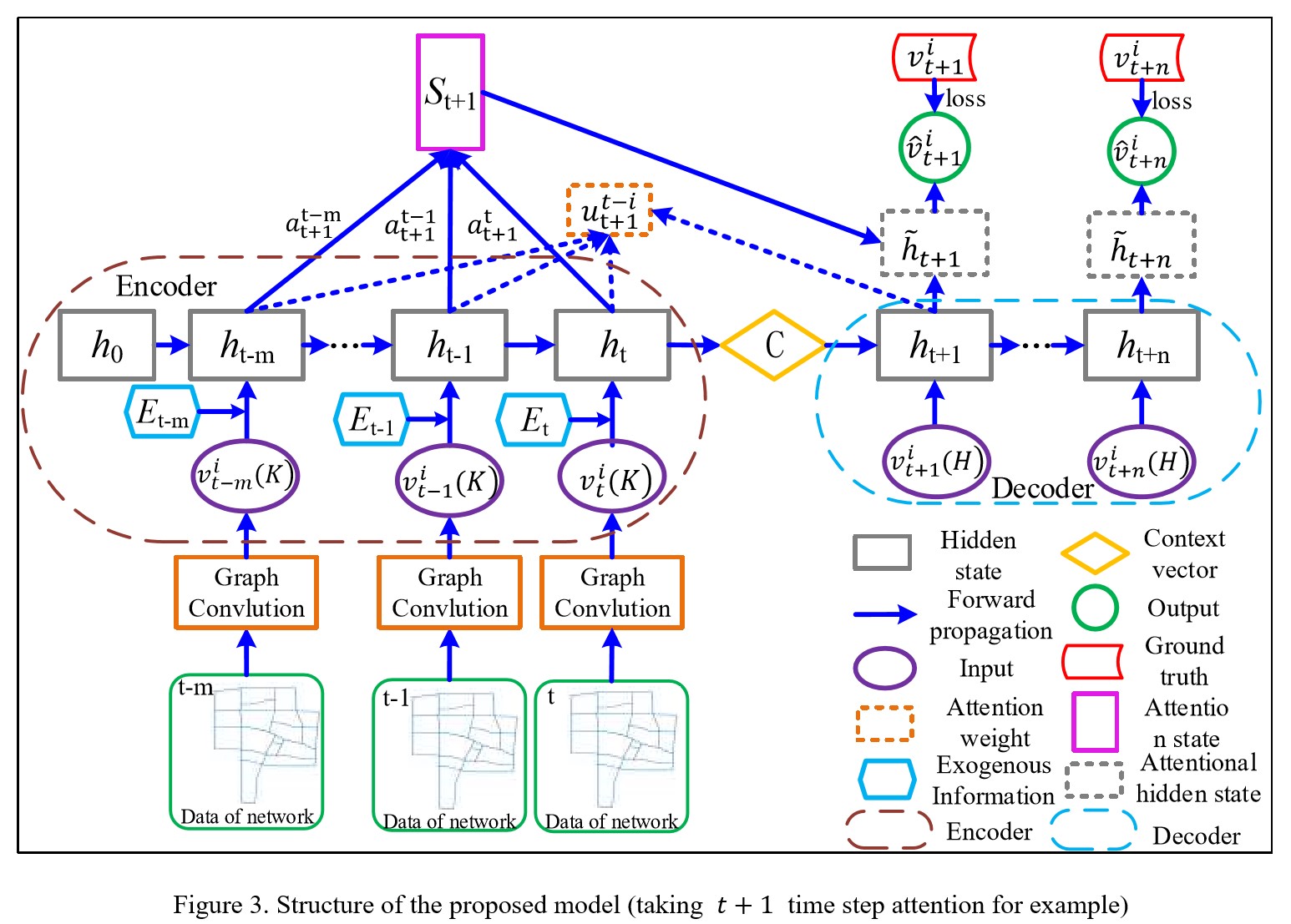
编码部分如式8-9，在时间步 $t-j, j\in \lbrace 0, \dots, m \rbrace$，前一个隐藏状态 $\boldsymbol{h}_{t-j-1}$ 传入到当前时间戳和 $\boldsymbol{X}_{t-j}$ 计算得到 $\boldsymbol{h}_{t-j}$。因此，背景向量 $\boldsymbol{C}$ 存储了包括隐藏状态 $(\boldsymbol{h}_{t-m}, \boldsymbol{h}_{t-m+1}, \boldsymbol{h}_{t-1})$ 和输入向量 $(\boldsymbol{X}_{t-m}, \boldsymbol{X}_{t-m+1}, \boldsymbol{X}_t)$ 的信息。

$$\tag{8} \boldsymbol{h}_{t-j} = \begin{cases} \text{Cell}_{encoder}(\boldsymbol{h}_0, \boldsymbol{X}_{t-j}), \quad &j = m\\ \text{Cell}_{encoder}(\boldsymbol{h}_{t-j-1}, \boldsymbol{X}_{t-j}), \quad &j \in \lbrace 0, \dots, m-1 \rbrace \end{cases}$$ $$\tag{9} \boldsymbol{C} = \boldsymbol{h}_t$$

其中 $\boldsymbol{h}_0$ 是初始隐藏状态，通常是 0 向量；$\text{Cell}_{encoder}(·)$ 是编码器的计算函数，由使用的 RNN 结构决定。

在解码器的部分，关键是利用背景向量 $\boldsymbol{C}$ 作为初始的隐藏向量，一步一步地解码。时间 $t+j, j \in \lbrace 1, \dots, n \rbrace$ 步，隐藏状态 $\boldsymbol{h}_{t+j}$ 不仅包括输入信息，还考虑之前的输出状态 $(\boldsymbol{h}_{t+1}, \boldsymbol{h}_{t+2}, \dots, \boldsymbol{h}_{t+j-1})$。

解码器的输入依赖于训练方法。Teacher forcing 在 NLP 中是一个流行的训练策略。在 teacher-forcing 训练策略中，真值在训练的时候输入到解码器，测试的时候将预测值输入进解码器。这种方法不适合时间序列预测主要是因为在训练和测试的时候，输入到解码器的分布不一致。Li et al. (2017) 使用 scheduled sampling 缓解了这个问题，通过设定概率 $\epsilon$，随机的将真值或预测值放入到解码器中。但这会增加模型的复杂度，给计算造成负担。

为了解决这个问题，我们提出了一个新的训练策略，将历史的统计信息和时间信息作为输入。在时间序列预测问题中，历史信息可以通过训练和测试阶段获得；这样解码器在训练和测试的时候，其输入的分布就可以相互同步，解决 teacher forcing 的问题。此外，因为历史统计信息在多步预测中很重要，增加这个可以提高模型的预测精度。下面的等式用来计算 $t+j,j \in \lbrace 1, \dots, n \rbrace$ 这个时间步解码器的隐藏状态。

$$\tag{10} \boldsymbol{v}^i_{t+j}(H) = [N_{t+j}; v^i_{t+j, average};v^i_{t+j, median}; v^i_{t+j, max}; v^i_{t+j, min}; d^i_{t+j}]$$ $$\tag{11} \boldsymbol{h}_{t+j} = \begin{cases} \text{Cell}_{decoder}(\boldsymbol{C}, \boldsymbol{v}^i_{t+j}(H)), \quad &j = 1\\ \text{Cell}_{decoder}(\boldsymbol{h}_{t+j-1}, \boldsymbol{v}^i_{t+j}(H)), \quad &j \in \lbrace 2, \dots, n \rbrace \end{cases}$$

其中 $\text{Cell}_{decoder}$ 是解码器的计算公式，与编码器类似。

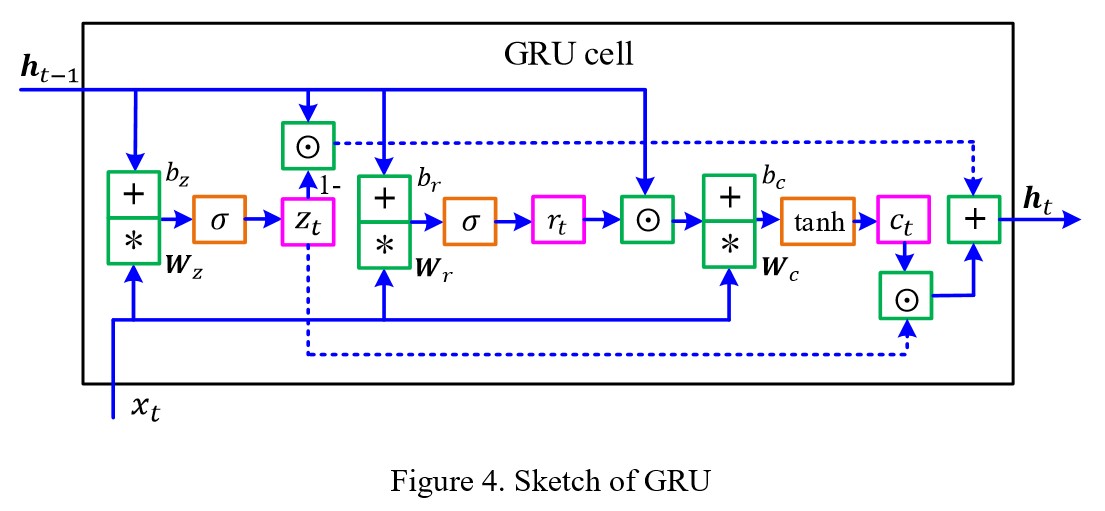
我们使用 GRU (Chung et al., 2014) 作为编码和解码的结构，如图4。实验效果比标准的 LSTM 好很多。编码器和解码器的计算过程如式12-17所示：

$$\tag{12} z_t = \sigma(\boldsymbol{W}_z \cdot [\boldsymbol{h}_{t-1}; x_t] + b_z)$$ $$\tag{13} r_t = \sigma(\boldsymbol{W}_r \cdot [\boldsymbol{h}_{t-1}; x_t] + b_r)$$ $$\tag{14} c_t = \text{tanh}(\boldsymbol{W}_c \cdot [r_t \odot \boldsymbol{h}_{t-1}; x_t] + b_c)$$ $$\tag{15} \boldsymbol{h}_t = (1 - z_t) \odot \boldsymbol{h}_{t-1} + z_t \odot c_t$$ $$\tag{16} \sigma(x) = \frac{1}{1 + e^{-x}}$$ $$\tag{17} \text{tanh}(x) = \frac{e^x - e^{-x}}{e^x+e^{-x}}$$

在上式中，$z_t$ 和 $r_t$ 分别是更新门和重置门。$c_t$ 是候选输出，$\sigma(\cdot)$ 和 $\text{tanh}(\cdot)$ 是两个激活函数。$W_z$，$W_r$ 和 $W_c$ 是权重矩阵，$b_z$，$b_r$ 和 $b_c$ 是偏置。

为了捕获交通模式的外部信息，我们还集成了注意力机制 (Bahdanau et al., 2014; Luong et al., 2015)。注意力机制的关键在于在每个时间步增加捕获了源信息的相关性的注意力向量来帮助交通速度。在时间步 $t+j, j \in \lbrace 1, \dots, n \rbrace$，注意力函数定义为式 18-20，将 query $\boldsymbol{h}_{t+j}$ 和 一组 key $(\boldsymbol{h}_{t-m}, \dots, \boldsymbol{t-1}, \boldsymbol{h}_t)$ 映射起来组成注意力向量 $\boldsymbol{S}_{t+j}$。如下式 18-20，$\boldsymbol{S}_{t+j}$ 通过计算这些 key 的带权和得到，权重通过计算得到：

$$\tag{18} u^{t-i}_{t+j} = \boldsymbol{q}^T \text{tanh} (\boldsymbol{h}_{t+j} \boldsymbol{W}_f \boldsymbol{h}_{t-j}), \quad i = 0,1,\dots,m$$ $$\tag{19} a^{t-i}_{t+j} = \text{softmax}(u^{t-i}_{t+j}) = \frac{\text{exp}(u^{t-i}_{t+j})}{\sum^m_{r=1} \text{exp} (u^{t-r}_{t+j})}, \quad i=0,1,\dots,m$$ $$\tag{20} \boldsymbol{S}_{t+j} = \sum^m_{i=1} a^{t-i}_{t+j} \boldsymbol{h}_{t-i}$$

其中，式 18 计算出的 $u^{t-i}_{t+j}$ 可以用来衡量 $\boldsymbol{h}_{t+j}$ 和 $\boldsymbol{h}_{t-i}$ 之间的相似性，我们使用 Luong Attention form (Luong et al., 2015) 作为注意力的计算公式，$\boldsymbol{W}_f$ 和 $\boldsymbol{q}^T$ 是参数，用来调节结果的维数；$a^{t-i}_{t+j}$ 是 $u^{t-i}_{t+j}$ 归一化的结果，用作对应编码器隐藏状态 $\boldsymbol{h}_{t-i}$ 的权重来计算 $\boldsymbol{S}_{t+j}$。

如图3所示，注意力隐藏状态 $\tilde{\boldsymbol{h}}_{t+j}$ 由注意力向量 $\boldsymbol{S}_{t+j}$ 和原始隐藏状态 $\boldsymbol{h}_{t+j}$ 通过一个简单拼接组成，如式 21 所示。式 22 表示从隐藏状态到输出的线性变换。参数 $\boldsymbol{W}_v$ 和 $b_v$ 的维度与输出一致。

$$\tag{21} \tilde{\boldsymbol{h}}_{t+j} = \text{tanh} (\boldsymbol{W}_h \cdot [\boldsymbol{S}_{t+k};\boldsymbol{h}_{t+j}])$$ $$\tag{22} \hat{v}_{t+j} = \boldsymbol{W}_v \tilde{h}_{t+j} + b_v$$

为了减少多步预测中的误差，我们定义了所有要预测的时间步上的平均绝对误差：

$$\tag{23} loss = \frac{1}{n} \sum^n_{j=1} \vert \hat{v}^i_{t+j} - v^i_{t+j} \vert$$

所有的参数通过随机梯度下降训练。

4 NUMERICAL EXAMPLES

4.1 Dataset

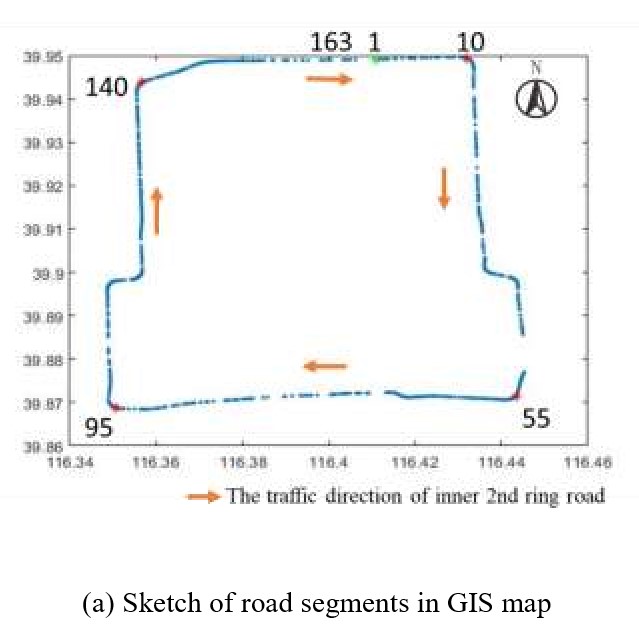
数据集是从 A-map 的用户收集的，是中国的一个手机导航应用提供的 (Sohu, 2018)。研究范围选择在了北京 2 环，是北京最堵的地方。如图5(a)所示，我们将 33km 长的二环以 200m 一段分成 163 个路段。此外，我们通过用户的轨迹点计算每个路段上 5 分钟的平均速度。2环上工作和和周末的车速如图5(b)(c)所示，x 轴是经度，y 轴是纬度，z 轴是时间和速度的颜色表。

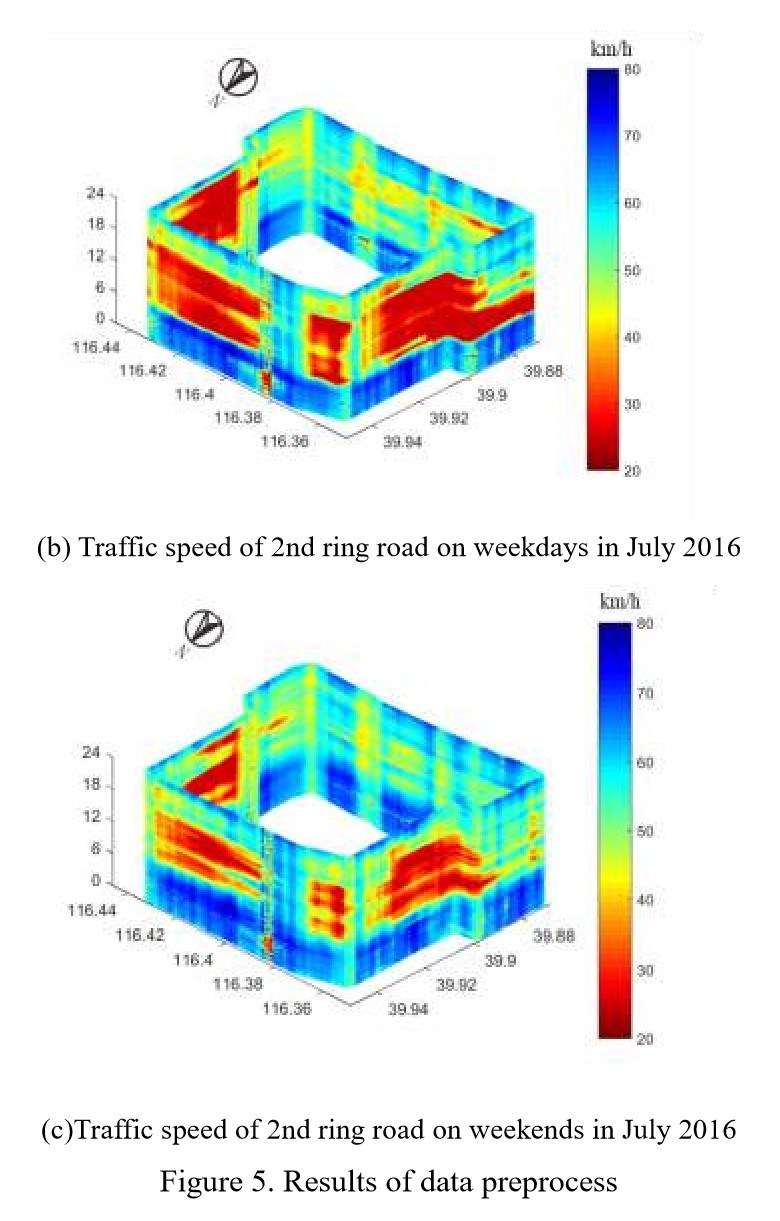
数据范围是2016年10月1日到2016年11月30日。10月1日到11月20日做训练，11月21日到27日做测试。预测的范围是 06:00 到 22:00，因此，每条路段每天包含 192 个数据点。图6展示了划分的数据集。在数据清理后，缺失值通过线性插值的方法填补。

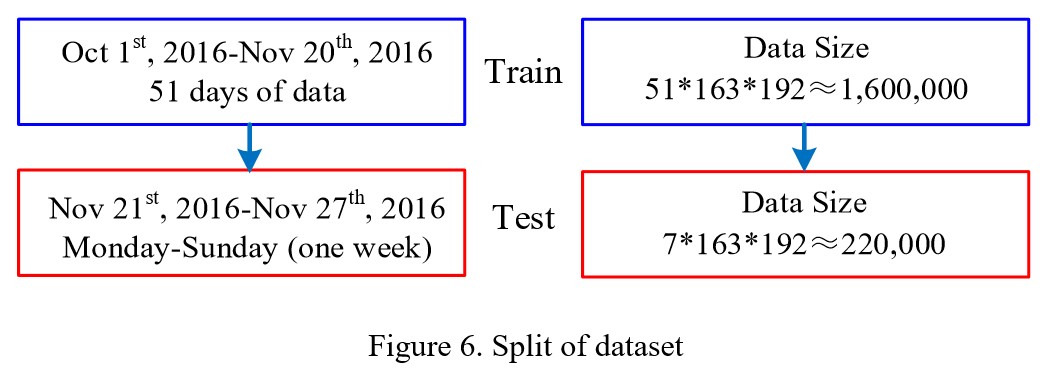
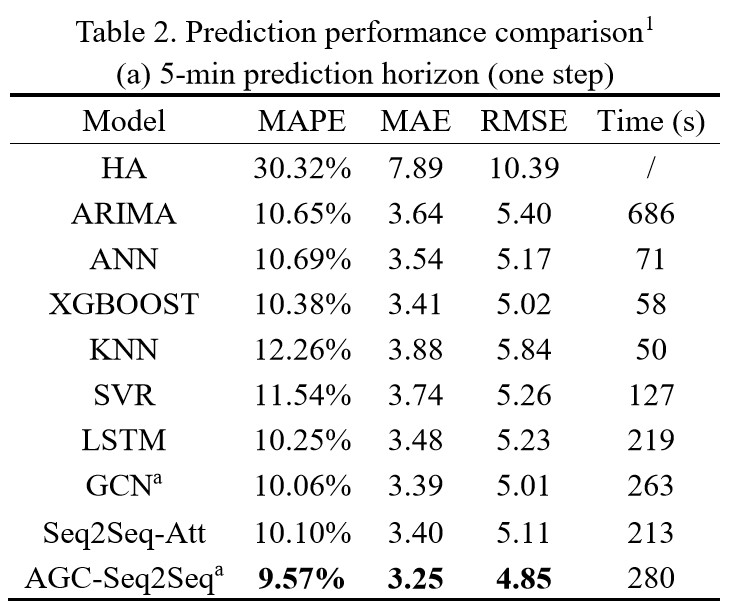
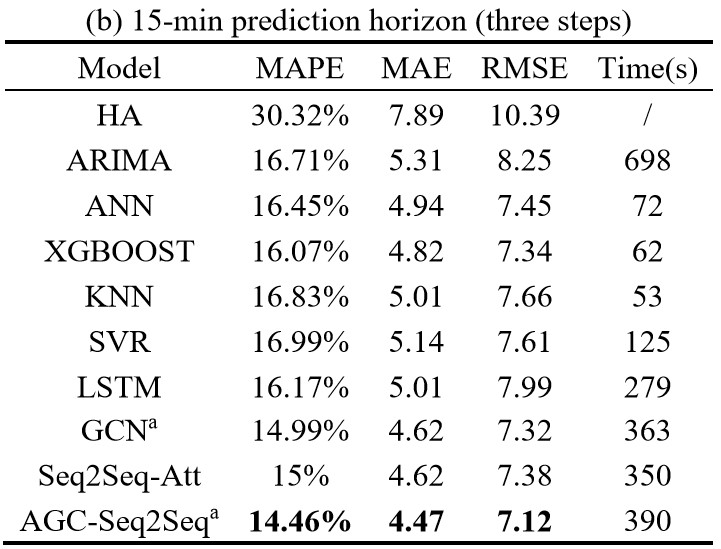
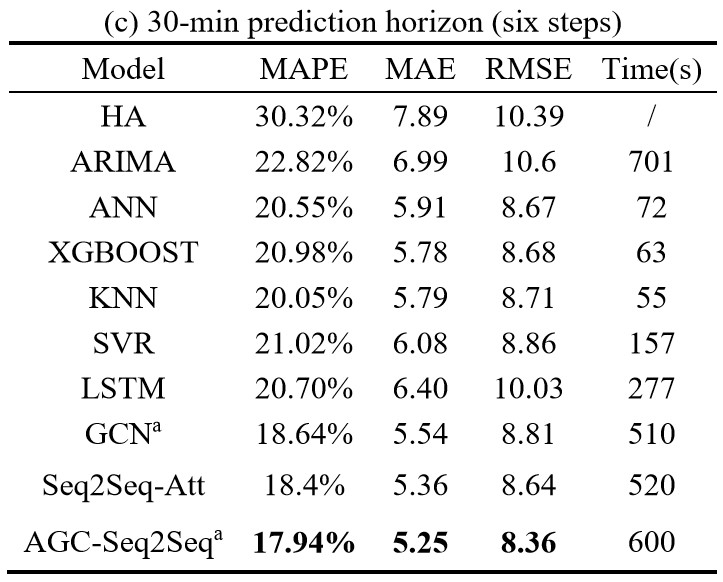
4.2 Model comparisons

在每个部分，提出的模型对比的是其他的 benchmark 模型，包括传统的时间序列分析方法（如 HA 和 ARIMA），还有一些先进的机器学习方法（ANN, KNN, SVR, XGBOOST），深度学习模型（LSTM, GCN, Seq2Seq-Att）。

• HA：历史均值模型通过训练集的统计值预测测试集的未来车速。举个例子，路段 $l_i \in \mathcal{L}$ 在 8:00-8:05 的平均车速通过训练集同时段同路段的历史速度均值估计。
• ARIMA：$(p, d, q)$ 模型 (Box and Pierce, 1970)，差分的阶数设定为 $d = 1$，自回归部分的阶数和移动平均部分的阶数 $(p, q)$ 通过计算对应的 Akaike information criterion 决定，$p \in [0, 2], q \in [7, 12]$。
• ANN：我们用了三层神经网络，sigmoid 激活，隐藏单元数是特征数的 2 倍。因为 ANN 不能区分时间步上的变量，所以它不能捕获时间依赖。
• KNN：k 近邻，获取训练集中特征空间最相近的 k 个观测值。预测值通过对应的特征向量进行线性组合得到。超参数 $K$ 通过 5 到 25 折的交叉验证选定。
• SVR：支持向量回归 (Suykens and Vandewalle, 1999)，通过核函数将特征向量映射到高维空间得到拟合曲线。核函数和超参数通过交叉验证选定。
• XGBOOST：(Chen and Guestrin, 2016) 在很多机器学习任务上表现出了很好的效果；基于树结构可以扩展成端到端的系统。所有的特征 reshape 后输入到 XGBOOST 来训练。
• LSTM：(Hochreiter and Schmidhuber, 1997)，每个路段的所有特征都 reshape 成一个矩阵，一个轴是时间，另一个轴是特征。LSTM 考虑时间依赖，但是没有捕获空间依赖。
• GCN：GCN 中所有的路段的特征 reshape 成一个矩阵，一个轴是路段，另一个轴是特征。GCN 通过拉普拉斯矩阵将卷积泛化到非欧空间；因此，只考虑了空间关联，没有捕获时间依赖。
• Seq2Seq-Att: 和 AGC-Seq2Seq 的区别是图卷积层。

为了保证共鸣，之前提到的预测模型都有和 AGC-Seq2Seq 同样的输入特征（特征类型和窗口长度），尽管传统的时间序列模型利用了训练集的全部速度记录。窗口长度为 12，也就是用过去一小时预测未来。19 维特征如表 1 所示。

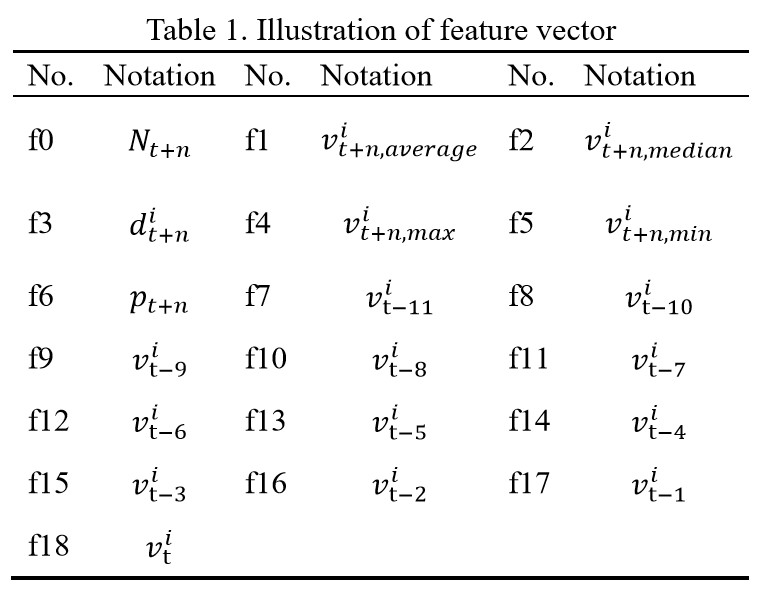
所有的符号如 3.1 节定义，$n$ 是定值。我们通过三个错误指标评价模型，MAPE, MAE, RMSE, $\text{MAPE} = \frac{1}{Q} \sum^Q_{i=1} \frac{\vert v_i - \hat{v}_i \vert}{v_i}$, $\text{MAE} = \frac{1}{Q} \sum^Q_{i=1} \vert v_i - \hat{v}_i \vert$, $\text{RMSE} = \sqrt{\frac{1}{Q} \sum^Q_{i=1} (v_i - \hat{v}_i)^2}$，其中 $v_i$ 和 $\hat{v}^i$ 分别是真值和预测值；$Q$ 是测试集大小。