GMAN: A Graph Multi-Attention Network for Traffic Prediction

AAAI 2020，使用编码解码+att的架构，只不过编码和解码都使用 attention 组成。主要的论点是空间和时间的关联性是动态的，所以设计这么一个纯注意力的框架。值得注意的点是：由于注意力分数的个数是平方级别的，在计算空间注意力的时候，一旦结点数很大，这里会有超大的计算量和内存消耗，这篇文章是将结点分组后，计算组内注意力和组间注意力。原文链接：https://arxiv.org/abs/1911.08415。

Abstract

长时间范围的交通流预测是个挑战，两方面原因：交通系统的复杂性，很多影响因素的持续变化性。我们在这篇论文中，专注于时空因素，提出了一个图多注意力机智网络（GMAN），预测路网上不同区域的交通状况。GMAN 使用一个编码解码结构，编码解码器都由多个时空注意力块组成，时空注意力块对交通状况上的时空因素的影响建模。编码器将输入的交通特征编码，解码器输出预测序列。编码解码器之间，有一个变换注意力层，用来把编码器编码后的交通特征生成成未来时间步的序列表示，然后把这个表示输入到解码器里面。变换注意力机制对历史和未来时间步的关系建模，可以减轻多步预测中的错误积累。两个真实数据集上的交通预测任务（一个是流量预测，一个是速度预测）显示 GMAN 的效果优越。在1小时的预测上，GMAN 在 MAE 比 state-of-the-art 好4%。源码在：https://github.com/zhengchuanpan/GMAN

Introduction

交通预测的目标是基于历史观测预测未来的交通状况。在很多应用中扮演着重要的角色。举个例子，精确的交通预测可以帮助交管部门更好的控制交通，减少拥堵。

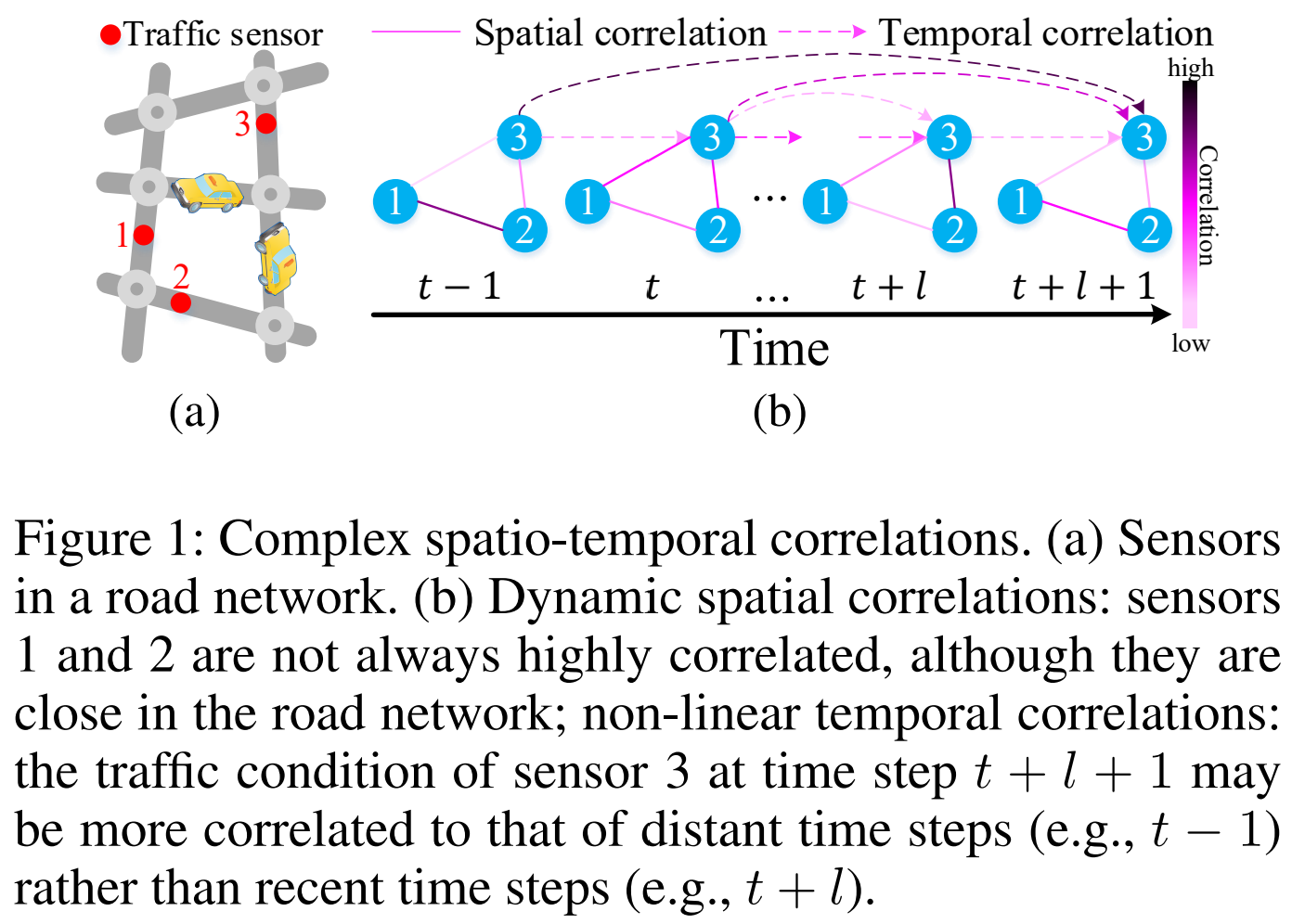
邻近区域的交通状况会互相影响。大家使用 CNN 捕获这样的空间依赖。同时，一个地方的交通状况和它的历史记录有关。RNN 广泛地用于这样时间相关性的建模。最近的研究将交通预测变为图挖掘问题，因为交通问题受限于路网。使用 GCN 的这些研究在短期预测（5 到 15 分钟）内表现出不错的效果。然而，长期预测（几个小时）仍缺乏令人满意的效果，主要受限于以下几点：

1) 复杂的时空关联：

• 动态的空间关联。如图 1 所示，路网中的传感器之间的关联随时间剧烈地变化，比如高峰时段的前后。如何动态地选择相关的检测器数据来预测一个检测器在未来长时间范围的交通状况是一个挑战。
• 非线性的时间关联。图 1，一个检测器的交通状况可能变化得非常剧烈，且可能由于事故等因素，突然影响不同时间步之间的关联性。如何自适应地随时间的推移对这种非线性时间关联建模，也是一个挑战。

2) 对误差传递的敏感。长期预测上，每个时间步上小的错误都会被放大。这样的误差传递对于远期时间预测来说仍具有挑战性。

为了解决上述挑战，我们提出了一个图多注意力网络（GMAN）来预测未来的交通状况。这里指的交通状况是一个交通系统中可以记录为数值的观测值。为了描述，我们这里专注于流量和速度预测，但是我们的模型是可以应用到其他数值型的交通数据上的。

GMAN 使用编码解码架构，编码器编码交通特征，解码器生成预测序列。变换注意力层用来把编码历史特征转换为未来表示。编解码器都由一组时空注意力块 ST-Attention blocks 组成。每个时空注意力块由一个空间注意力、一个时间注意力和一个门控融合机制组成。空间注意力建模动态空间关联，时间注意力建模非线性时间关联，门控融合机制自适应地融合空间和时间表示。变换注意力机制建模历史和未来的关系，减轻错误传播。两个真实世界数据集证明 GMAN 获得了最好的效果。

我们的贡献

• 提出空间注意力和时间注意力对动态空间和非线性时间关联分别建模。此外，我们设计了一个门控融合机制，自适应地融合空间注意力和时间注意力机制的的信息。
• 提出一个变换注意力机制将历史交通特征转换为未来的表示。这个注意力机制对历史和未来的关系直接建模，减轻错误传播的问题。
• 我们在两个数据集上评估了我们的图多注意力网络，在 1 小时预测问题上比 state-of-the-art 提高了 4%。

Preliminaries

路网表示为一个带全有向图 $\mathcal{G} = (\mathcal{V}, \mathcal{E}, \mathcal{A})$。$\mathcal{V}$ 是 $N$ 个结点的集合；$\mathcal{E}$ 是边集；$\mathcal{A} \in \mathbb{R}^{N \times N}$ 是邻接矩阵，表示结点间的相似性，这个相似性是结点在路网上的距离。

时间步 $t$ 的路网状况表示为图信号 $X_t \in \mathbb{R}^{N \times C}$，$C$ 是特征数。

研究的问题：给定 $N$ 个结点历史 $P$ 个时间步的观测值 $\mathcal{X} = (X_{t_1}, X_{t_2}, \dots. X_{t_P}) \in \mathbb{R}^{P \times N \times C}$，我们的目标是预测未来 $Q$ 个时间步所有结点的交通状况，表示为 $\hat{Y} = (\hat{X}_{t_{P+1}}, \hat{X}_{t_{P+2}}, \dots, \hat{X}_{t_{P+Q}}) \in \mathbb{R}^{Q \times N \times C}$。

Graph Multi-Attention Network

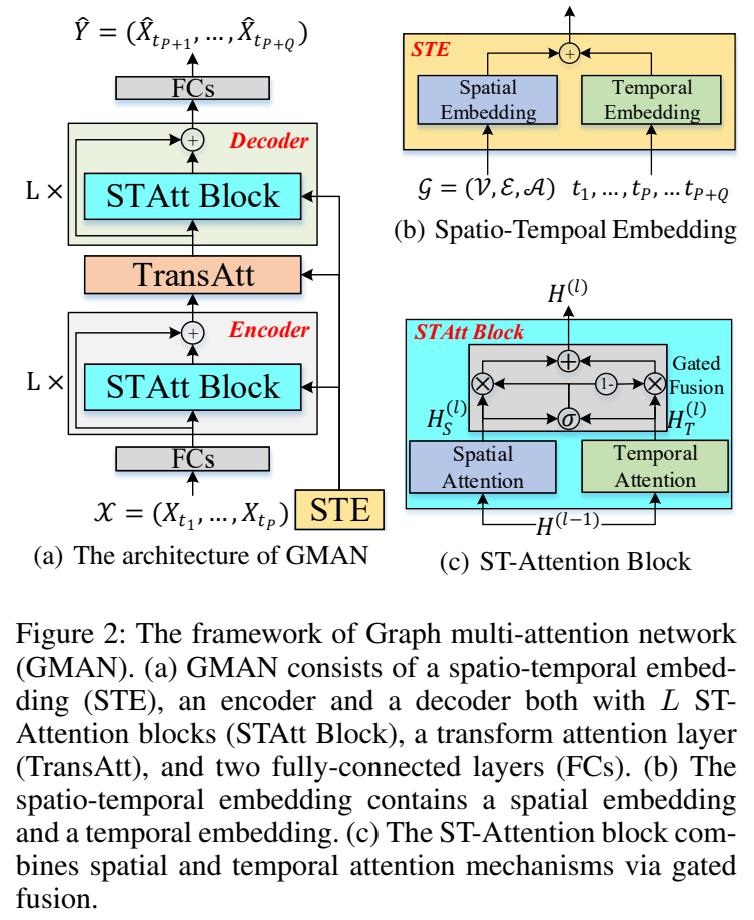
图 2 描述了我们模型的架构。编码和解码器都有 STAtt Block 和残差连接。每个 ST-Attention block 由空间注意力机制、时间注意力机制和一个门控融合组成。编码器和解码器之间有个变换注意力层。我们还通过一个时空嵌入 spatial-temporal embedding (STE) 继承了图结构和时间信息到多注意力机制中。此外，为了辅助残差连接，所有层的输出都是 D 维。

Spatio-Temporal Embedding

因为交通状况的变化受限于路网，集成路网信息到模型中很重要。为此，我们提出一个空间嵌入，把结点嵌入到向量中以此保存图结构信息。我们利用 node2vec 学习结点表示。此外，为了协同训练模型和预学习的向量，这些向量会放入一个两层全连接神经网络中。然后就可以拿到空间表示 $e^S_{v_i} \in \mathbb{R}^D$。

空间嵌入只提供了固定的表示，不能表示路网中的传感器的动态关联性。我们提出了一个时间嵌入来把每个时间步编码到向量中。假设一天是 T 个时间步。我们使用 one-hot 编码星期、时间到 $\mathbb{R}^7$ 和 $\mathbb{R}^T$ 里面，然后拼接，得到 $\mathbb{R}^{T + 7}$。接下来，使用两层全连接映射到 $\mathbb{R}^D$。在我们的模型里面，给历史的 $P$ 个时间步和未来的 $Q$ 个时间步嵌入时间特征，表示为 $e^T_{t_j} \in \mathbb{R}^D$，$t_j = t_1, \dots, t_P, \dots, t_{P+Q}$。

为了获得随时间变化的顶点表示，我们融合了上述的空间嵌入和时间嵌入，得到时空嵌入（STE），如图 2b 所示。结点 $v_i$ 在时间步 $t_j$，STE 定义为 $e_{v_i,t_j} = e^S_{v_i} + e^T_{t_j}$。因此，$N$ 个结点在 $P + Q$ 的时间步里的 STE 表示为 $E \in \mathbb{R}^{(P + Q) \times N \times D}$。STE 包含图结构和时间信息。它会用在空间、时间、变换注意力机制里面。

ST-Attention Block

我们将第 $l$ 个块的输入表示为 $H^{(l-1)}$，结点 $v_i$ 在时间步 $t_j$ 的隐藏状态表示为 $h^{(l-1)}_{v_i,t_j}$。第 $l$ 块中的空间和时间注意力机制的输出表示为 $H^{(l)}_S$ 和 $H^{(l)}_T$，隐藏状态表示为 $hs^{(l)}_{v_i,t_j}$ 和 $ht^{(l)}_{v_i,t_j}$。门控融合后，第 $l$ 层的输出表示为 $H^{(l)}$。

我们将非线性变换表示为：

$$\tag{1} f(x) = \text{ReLU}(x\mathbf{W} + \mathbf{b}).$$

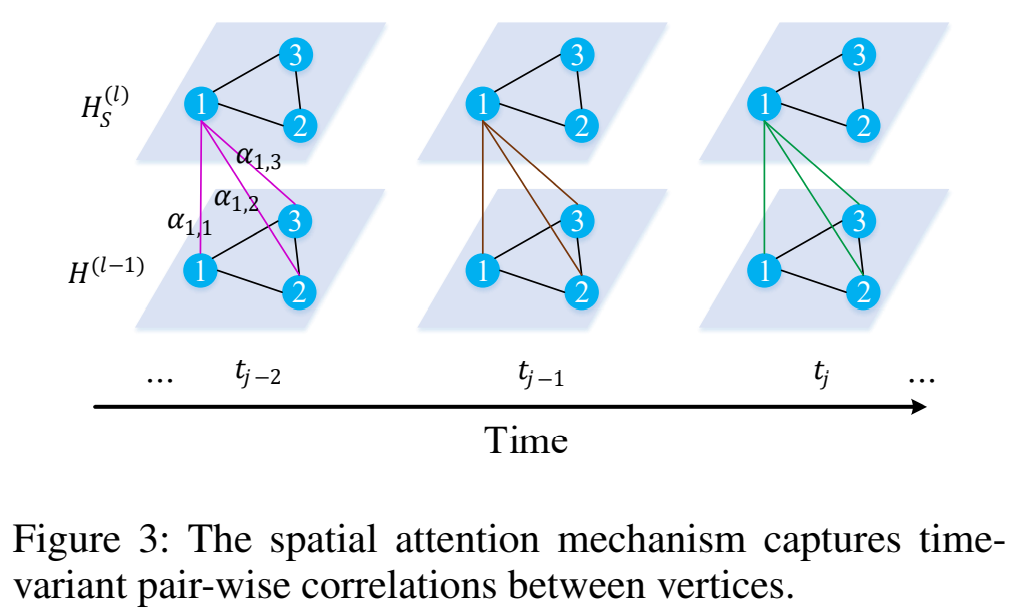
Spatial Attention 一条路的交通状况受其他路的影响，且影响不同。这样的影响是高度动态的，随时间变化。为了建模这些属性，我们设计了一个空间注意力机制动态地捕获路网中传感器间的关联性。核心点是在不同的时间步动态地给不同的结点分配权重，如图 3 所示。对于时间步 $t_j$ 的结点 $v_i$，我们计算所有结点的带权和：

$$\tag{2} hs^{(l)}_{v_i,t_j} = \sum_{v \in \mathcal{V}} \alpha_{v_i, v} \cdot h^{(l-1)}_{v,t_j},$$

$\alpha_{v_i, v}$ 是结点 $v$ 对 $v_i$ 的注意力分数，注意力分数之和为1：$\sum_{v \in \mathcal{V}} \alpha_{v_i, v} = 1$。

在一个确定的时间步，当前交通状况和路网结构能够影响传感器之间的关联性。举个例子，路上的拥挤可能极大地影响它临近路段的交通状况。受这个直觉的启发，我们考虑使用交通特征和图结构两方面来学习注意力分数。我们把隐藏状态和时空嵌入拼接起来，使用 scaled dot-product approach (Vaswani et al. 2017) 来计算结点 $v_i$ 和 $v$ 之间的相关性：

$$\tag{3} s_{v_i, v} = \frac{< h^{(l-1)}_{v_i,t_j} \Vert\ e_{v_i,t_j}, h^{(l-1)}+{v,t_j}, \Vert e_{v,t_j} >}{\sqrt{2D}}$$

其中，$\Vert$ 表示拼接操作，$< \bullet, \bullet >$ 表示内积，$2D$ 表示 $h^{(l-1)}_{v_i,t_j} \Vert e_{v_i,t_j}$ 的维度。$s_{v_i,v}$ 通过 softmax 归一化：

$$\tag{4} \alpha_{v_i,v} = \frac{\text{exp}(s_{v_i,v})}{\sum_{v_r \in \mathcal{V}} \text{exp}(s_{v_i,v_r})}.$$

得到注意力分数 $\alpha_{v_i,v}$ 之后，隐藏状态通过公式 2 更新。

为了稳定学习过程，我们把空间注意力机制扩展为多头注意力机制。我们拼接 $K$ 个并行的注意力机制，使用不同的全连接映射：

$$\tag{5} s^{(k)}_{v_i,v} = \frac{< f^{(k)}_{s,1} (h^{(l-1)}_{v_i,t_j} \Vert e_{v_i,t_j}), f^{(k)}_{s,2} (h^{(l-1)}_{v,t_j} \Vert e_{v,t_j}) >}{\sqrt{d}},$$ $$\tag{6} \alpha^{(k)}_{v_i,v} = \frac{\text{exp}(s^{(k)}_{v_i,v})}{\sum_{v_r \in \mathcal{V}} \text{exp}(s^{(k)}_{v_i,v_r})},$$ $$\tag{7} hs^{(l)}_{v_i,t_j} = \Vert^K_{k=1} \lbrace \sum_{v \in \mathcal{V}} \alpha^{(k)}_{v_i,v} \cdot f^{(k)}_{s,3}(h^{(l-1)}_{v,t_j}) \rbrace,$$

其中 $f^{(k)}_{s,1}(\bullet), f^{(k)}_{s,2}(\bullet), f^{(k)}_{s,3}(\bullet)$ 表示第 $k$ 注意力头的三个不同的非线性映射，即公式 1 ，产生 $d = D / K$ 维的输出。

当结点数 $N$ 很大的时候，时间和内存消耗都会很大，达到 $N^2$ 的数量级。为了解决这个限制，我们提出了组空间注意力，包含了组内注意力分数和组间注意力分数，如图 4 所示。

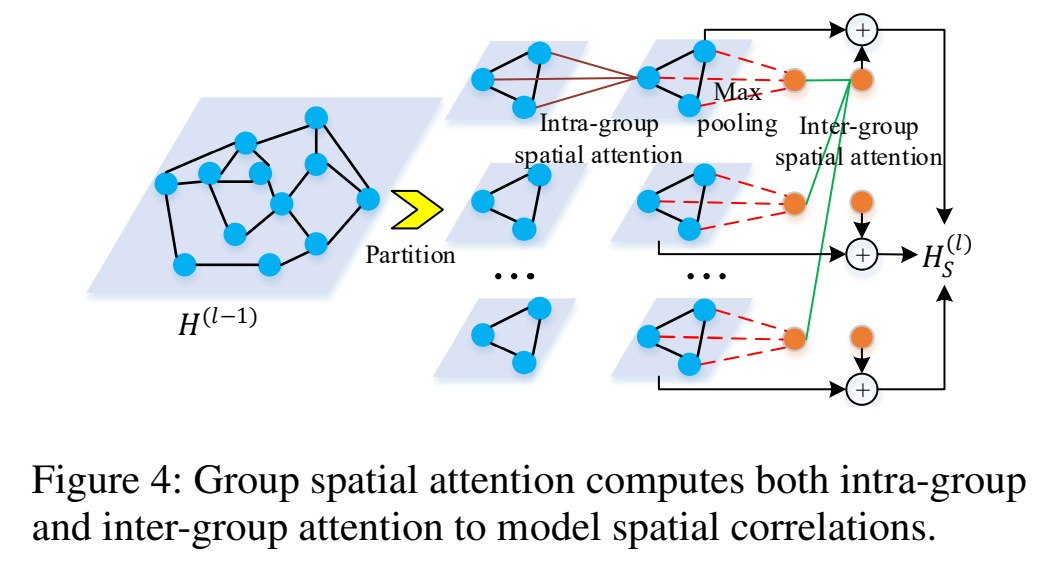
我们把 $N$ 个结点随机划分为 $G$ 个组，每个组包含 $M = N / G$ 个结点，如果必要的话可以加 padding。每个组，我们使用公式 5，6，7 计算组内的注意力，对局部空间关系建模，参数是对所有的组共享的。然后，我们在每个组使用最大池化得到每个组的表示。接下来计算组间空间注意力，对组间关系建模，给每个组生成一个全局特征。局部特征和全局特征相加得到最后的输出。

组空间注意力中，我们每个时间步需要计算 $GM^2 + G^2 = NM + (N / M)^2$ 个注意力分数。通过使梯度为0，我们知道 $M = \sqrt[3]{2N}$ 时，注意力分数的个数达到最大值 $2^{-1/3} N^{4/3} \ll N^2$。

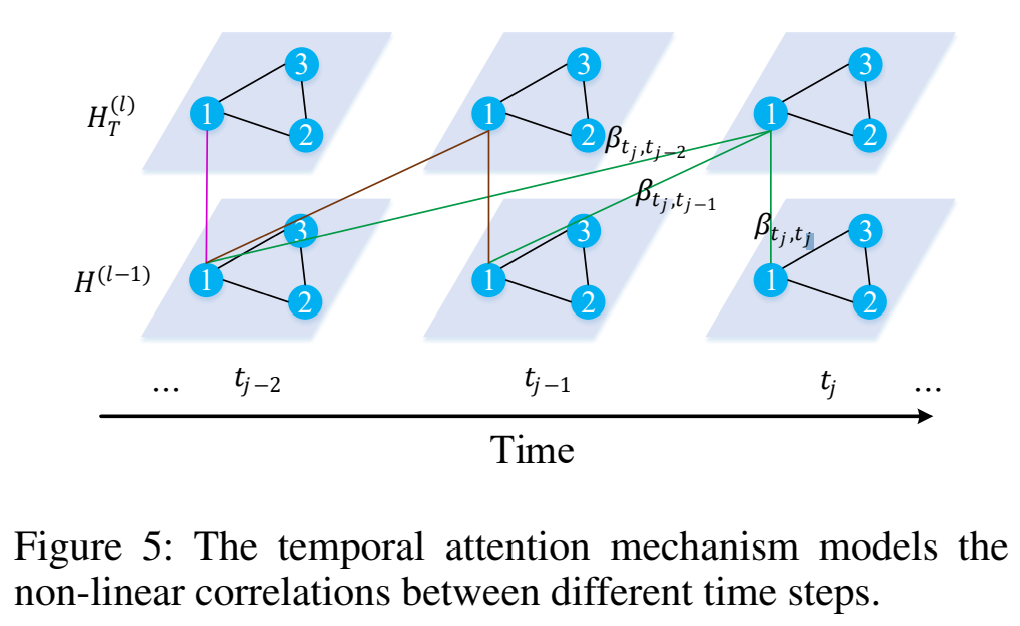
Temporal Attention 一个地点的交通状况和它之前的观测值有关，这个关联是非线性的。为了建模这些性质，我们设计了一个时间注意力机制，自适应地对不同时间步的非线性关系建模，如图 5 所示。可以注意到时间关联受到交通状况和对应的时间环境两者的影响。举个例子，早高峰的拥堵可能会影响交通好几个小时。因此，我们考虑交通特征和时间两者来衡量不同时间步的相关性。我们把隐藏状态和时空嵌入拼接起来，使用多头注意力计算注意力分数。对于结点 $v_i$，时间步 $t_j$ 与 $t$ 的相关性定义为：

$$\tag{8} u^{(k)}_{t_j,t} = \frac{< f^{(k)}_{t,1}(h^{(l-1)}_{v_i,t_j} \Vert e_{v_i,t_j}), f^{(k)}_{t,2}(h^{(l-1)}_{v_i,t} \Vert e_{v_i,t}) >}{\sqrt{d}},$$ $$\tag{9} \beta^{(k)}_{t_j,t} = \frac{\text{exp}(u^{(k)}_{t_j,t})}{\sum_{t_r \in \mathcal{N}_{t_j}}} \text{exp}(u^{(k)}_{t_j,t_r}),$$

$u^{(k)}_{t_j,t}$ 表示时间步 $t_j$ 和 $t$ 之间的相关性，$\beta^{(k)}_{t_j,t}$ 是第 $k$ 个头的注意力分数，表示时间步 $t$ 对时间步 $t_j$ 的重要性，两个 $f$ 是非线性变换，$\mathcal{N}_{t_j}$ 表示 $t_j$ 前的时间步的集合，即只考虑目标时间步以前的时间步，这样才有因果。一旦获得了注意力分数，时间步 $t_j$ 的结点 $v_i$ 的隐藏状态可以通过下面的公式更新：

$$\tag{10} ht^{(l)}_{v_i,t_j} = \Vert^K_{k=1} \lbrace \sum_{t \in \mathcal{N}_{t_j}} \beta^{(k)}_{t_j,t} \cdot f^{(k)}_{t,3}(h^{(l-1)}_{v_i,t}) \rbrace$$

$f$ 是非线性映射。公式 8，9，10 学习到的参数对所有结点和所有时间步共享，且并行计算。

Gated Fusion 一个时间步一条路上的交通状况与它自身之前的值和相邻道路上的交通状况相关。如图 2c 所示，我们设计了一个门控融合机制自适应地融合空间和时间表示。在第 $l$ 个块，空间和时间注意力的输出表示为 $H^{(l)}_S 和 $H^{(l)}_T$，两者的维度在编码器中是 $\mathbb{R}^{P \times N \times D}$，解码器中是 $\mathbb{R}^{Q \times N \times D}$。通过下式融合：

$$\tag{11} H^{(l)} = z \odot H^{(l)}_S + (1 - z) \odot H^{(l)}_T,$$ $$\tag{12} z = \sigma(H^{(l)}_S \mathbf{W}_{z,1} + H^{(l)}_T \mathbf{W}_{z,2} + \mathbf{b}_z),$$

门控融合机制自适应地控制每个时间步和结点上空间和时间依赖的流动。

Transform Attention

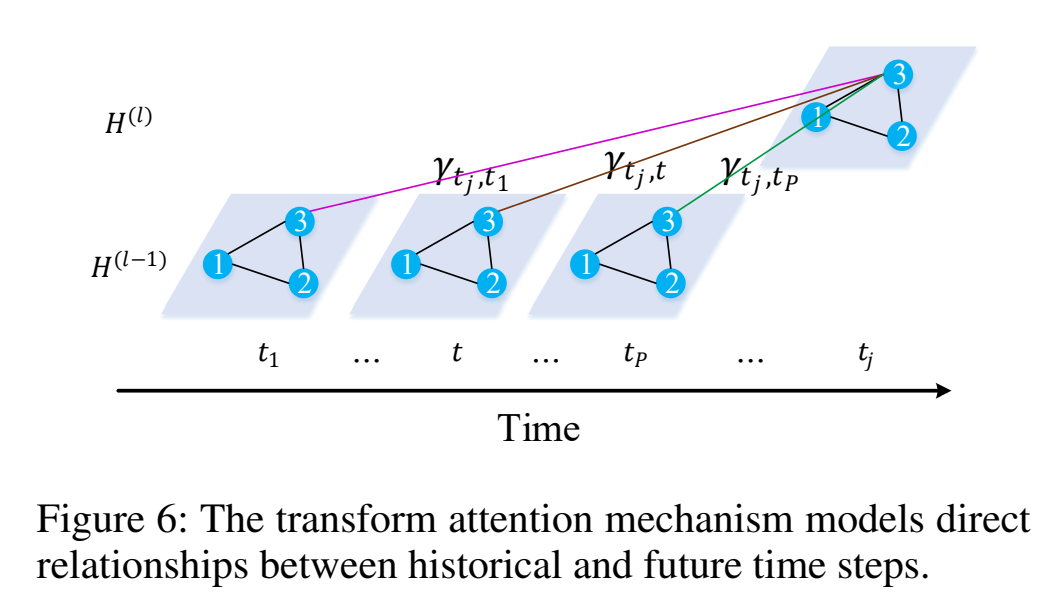
为了减轻错误传播的问题，我们在编码器和解码器之间加入了一个变换注意力层。它能直接地对历史时间步和未来时间步的关系建模，将交通特征编码为未来的表示，作为解码器的输入。如图 6 所示，对于结点 $v_i$ 来说，预测的时间步 $t_j \ (t_j = t_{P+1}, \dots, t_{P+Q})$ 和历史的时间步 $t \ (t_1, \dots, t_P)$ 通过时空嵌入来衡量：

$$\tag{13} \lambda^{(k)}_{t_j,t} = \frac{< f^{(k)}_{tr,1}(e_{v_i,t_j}), f^{(k)}_{tr,2}(e_{v_i,t}) >}{\sqrt{d}},$$ $$\tag{14} \gamma^{(k)}_{t_j,t} = \frac{\text{exp}(\lambda^{(k)}_{t_j,t})}{\sum^{t_P}_{t_r=t_1} \text{exp}(\lambda^{(k)}_{t_j,t_r})}.$$

编码的交通特征通过注意力分数 $\gamma^{(k)}_{t_j,t}$ 自适应地在历史 $P$ 个时间步选择相关的特征，变换到解码器的输入：

$$\tag{15} h^{(l)}_{v_i,t_j} = \Vert^K_{k=1} \lbrace \sum^{t_P}_{t=t_1} \gamma^{(k)}_{t_j,t} \cdot f^{(k)}_{tr,3}(h^{(l-1)}_{v_i,t}) \rbrace.$$

Encoder-Decoder

如图 2a 所示，GMAN 是编码解码架构。在进入编码器前，历史记录 $\mathcal{X} \in \mathbb{R}^{P \times N \times C}$ 通过全连接变换到 $H^{(0)} \in \mathbb{R}^{P \times N \times D}$。然后 $H^{(0)}$ 输入到 $L$ 个时空注意力块组成的编码器中，产生输出 $H^{(L)} \in \mathbb{R}^{P \times N \times D}$。然后变换注意力层把编码特征从 $H^{(L)}$ 转换为 $H^{(L+1)} \in \mathbb{R}^{Q \times N \times D}$。然后 $L$ 个时空注意力块的解码器产生输出 $H^{(2L + 1)} \in \mathbb{R}^{Q \times N \times D}$。最后，全连接层输出 $Q 个时间步的预测 $\hat{Y} \in \mathbb{R}^{Q \times N \times C}$。

GMAN 可以通过最小化 MAE 来优化：

$$\tag{16} \mathcal{L}(\Theta) = \frac{1}{Q} \sum^{t_{P + Q}}_{t = t_P + 1} \vert Y_t - \hat{Y}_t \vert,$$

$\Theta$ 表示可学习的参数。

Experiments

Datasets

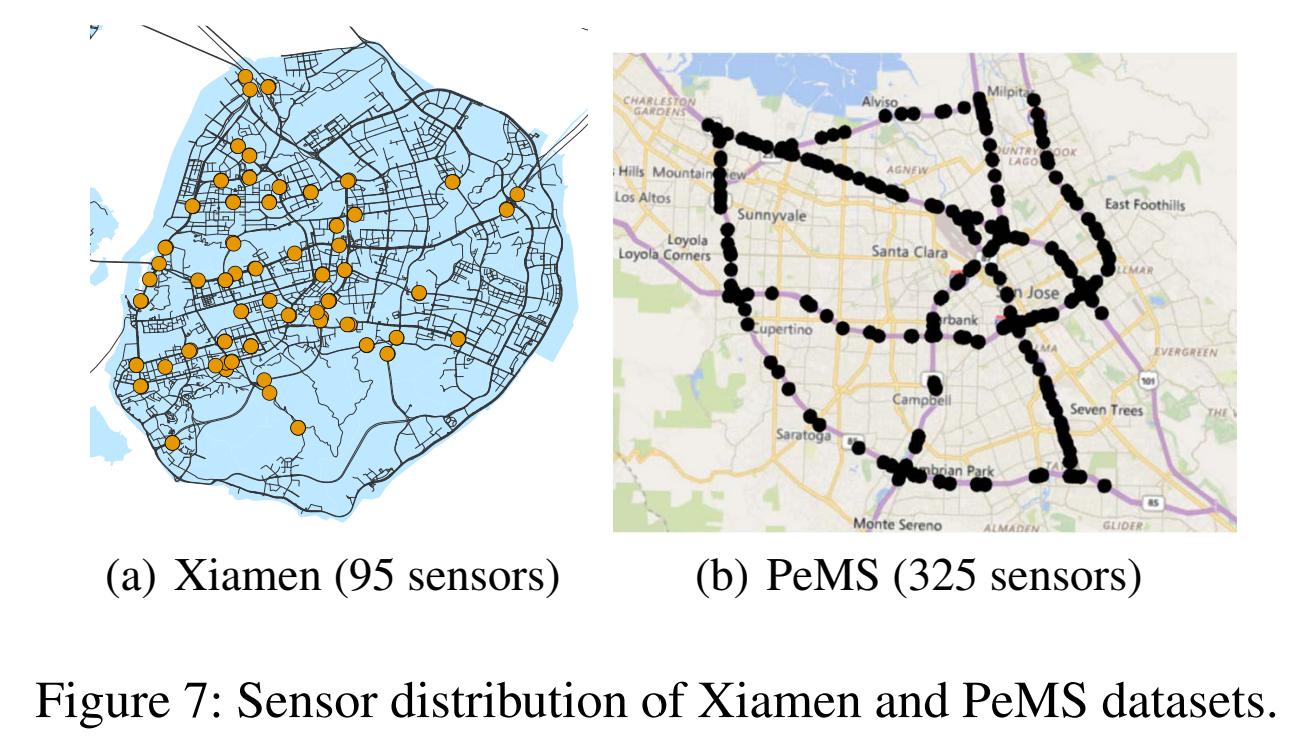
我们在两个不同规模的交通预测数据集上衡量了模型的效果：（1）厦门数据集，流量预测，包含 95 个传感器从 2015 年 8 月 1 日到 12 月 31 日 5 个月的数据；（2）PeMS 数据集上速度预测，包含 325 个传感器 6 个月的数据。检测器的分布如图 7.

Data Preprocessing

一个时间步表示 5 min，使用 Z-Score 归一化，70% 用于训练，10% 验证，20% 测试。我们计算路网上传感器之间的距离，使用如下的路网构建方法：

$$\tag{17} \mathcal{A}_{v_i,v_j} = \begin{cases} \text{exp}(- \frac{d^2_{v_i,v_j}}{\sigma^2}), & \text{if} \ \text{exp}(-\frac{d^2_{v_i,v_j}}{\sigma^2}) \geq \epsilon\\ 0, & \text{otherwise} \end{cases}$$

$\epsilon$ 设定为 0.1。

Experimental Settings

指标：MAE, RMSE, MAPE。

超参数就不描述了。

Baselines都是近几年的方法。

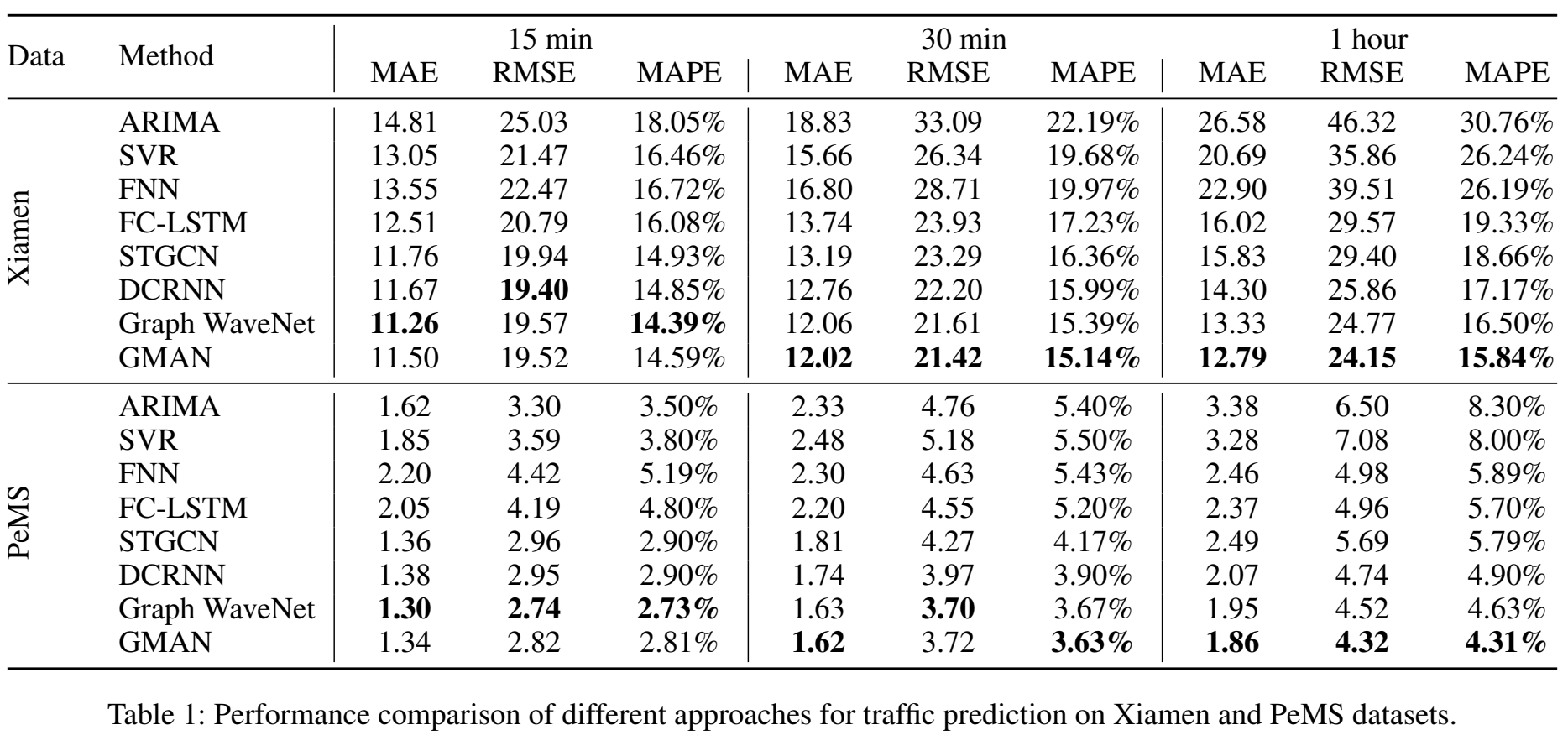
这里值得一提的是，最后一个训练和预测时间的比较，我个人认为脱离了框架或软件，单单比较每轮训练时长是毫无意义的，因为有些静态图框架它就是很快，动态图的就是慢，而且代码质量也有区别，有的代码质量高，自然就很快，代码质量低的就很慢。拿 Graph WaveNet 举例，他们公开的代码是 pytorch 的，而且他们在 inference 的时候要对 ground truth 进行反归一化，有的代码人家就不反归一化，这也会造成 inference 的时候有差别，且有的模型是随着结点数 $N$ 的增加模型有显著的耗时增加的现象，没有考虑这些就写 computation time 的比较我觉得没有什么用，何况以 AAAI 7 页的限制来说，完全说清楚这些也毫无意义。