Multi-Range Attentive Bicomponent Graph Convolutional Network for Traffic Forecasting
AAAI 2020,原文链接:https://arxiv.org/abs/1911.12093。
Abstract
交通预测在运输和公共安全中扮演重要角色,由于复杂的时空依赖和路网和交通状况带来的不确定性使这个问题很有挑战。最新的研究专注于使用图卷积网络 GCNs 对一个固定权重的图进行建模,即对空间依赖建模。然而,边,即两个结点之间的关系更加复杂且两者相互影响。我们提出了 Multi-Range Attentive Bicomponent GCN (MRA-BGCN),一种新的用于交通预测的深度学习框架。我们先根据路网上结点的距离构建结点图,在根据不同的边的交互模式构造边图。然后,我们使用 bicomponent 图卷积实现结点和边的交互。这个多范围注意力机制用来聚合不同邻居范围的信息,自动地学习不同范围的重要性。大量的实验在两个真实数据集,METR-LA 和 PEMS-BAY 上开展,显示出我们的模型效果很好。
Introduction
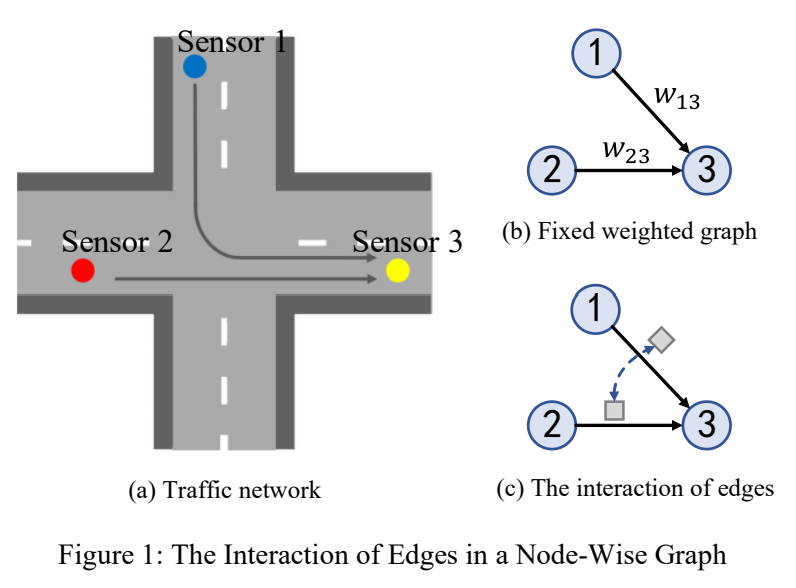
讲了好多历史。。。然后是论点部分:
我们认为 DCRNN 和 STGCN 虽说集成了 GCN,但是有两个点忽略了:
首先,这些方法主要关注通过在一个固定权重的图上部署 GCN 对空间依赖建模。然而,边更复杂。图 1a 中,传感器 1 和 3,还有 2 和 3,通过路网连接。显然,这些关联随当前的交通状况改变,他们之间也互相交互。图 1b 所示,现存的方法根据路网距离构建一个固定的带权图,使用 GCN 实现这些结点的交互,但是结点间的关联性在邻接矩阵中通过固定的值表示,这就忽略了边的复杂性和交互性。
其次,这些方法经常使用一个给定范围内聚合的信息,比如 $k$ 阶邻居,忽略多个范围的信息。然而,不同范围的信息表现出不同的交通属性。小的范围表现出局部依赖,大范围倾向于表现全局的交通模式。此外,不同范围的信息也不是永远都具有相同的分量。举个例子,一次交通事故,一个结点主要受它最近的邻居的影响,这样模型就应该更关注它,而不是给其他的 $k$ 阶邻居相同的关注。
为了解决上述两点问题,我们提出了 MRA-BGCN,不仅考虑结点关联,也把边作为实体,考虑他们之间的关系,如图 1c,我们还利用了不同的范围信息。我们的贡献:
- 提出 MRA-BGCN,引入 bicomponent 图卷积,对结点和边直接建模。结点图根据路网距离构建,边图根据边的交互模式、stream connectivity 和 竞争关系构建。
- 我们针对 bicomponent 图卷积提出多范围注意力机制,可以聚合不同范围邻居的信息,学习不同范围的重要性。
- 我们开展了大量的实验,实验效果很好。
Preliminaries
Problem Definition
给定历史的数据,预测未来的数据。$N$ 个结点组成的图 $G = (V, E, \bm{A})$。时间 $t$ 路网上的交通数据表示为图信号 $\bm{X}^{(t)} \in \mathbb{R}^{N \times P}$,$P$ 是特征数。交通预测是过去的数据预测未来:
$\bm{X}^{(t-T’+1):t} \in \mathbb{R}^{N \times P \times T’}$,$\bm{X}^{(t+1):(t+T)} \in \mathbb{R}^{N \times P \times T}$。
Graph Convolution
不介绍了。
Methodology
Model Overview
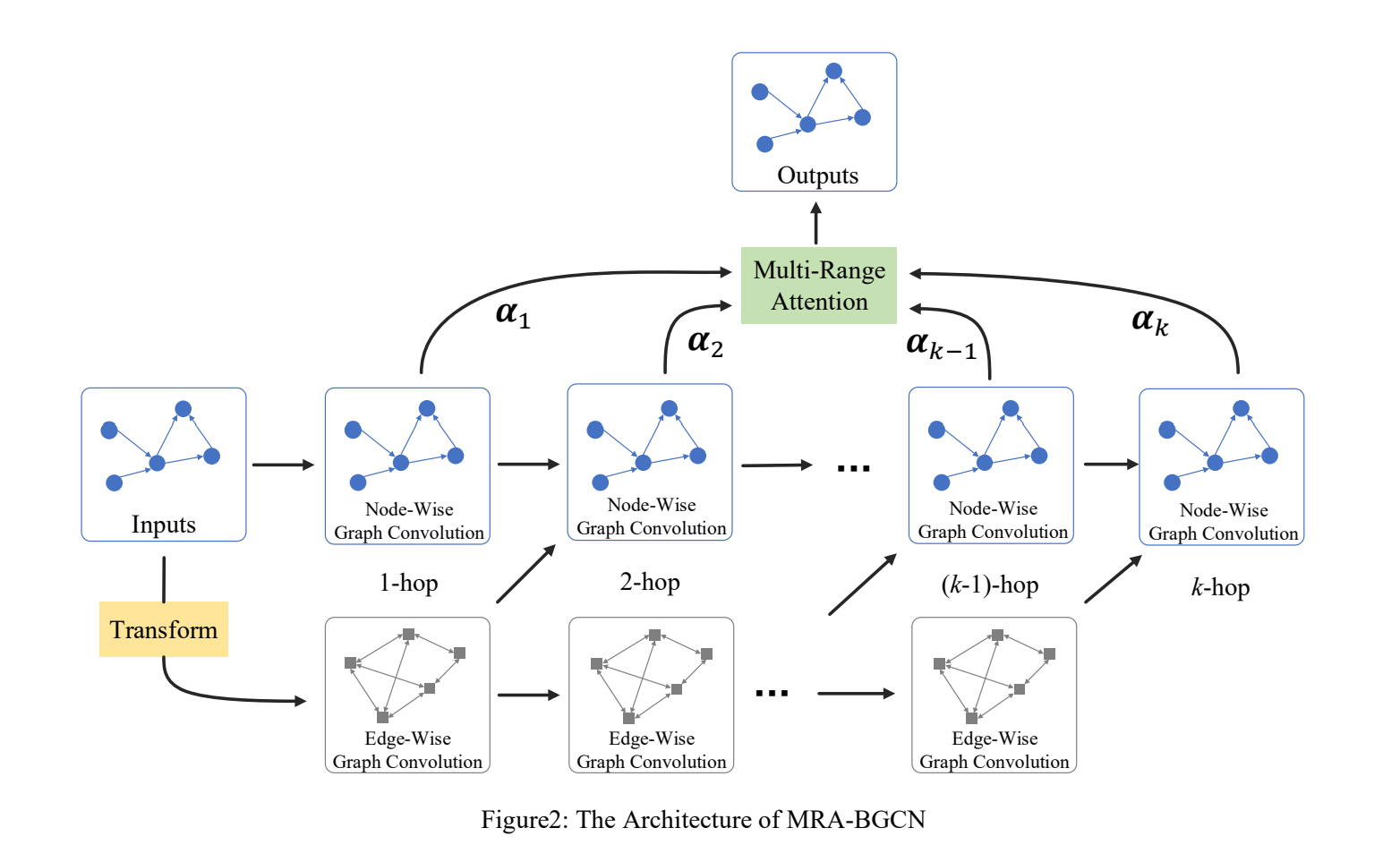
图 2 展示了 MRA-BGCN 的架构,包含两个部分:(1)双组件图卷积模块;(2)多范围注意力层。双组件图卷积模块包含多个结点图卷积层和边图卷积层,直接对结点和边的交互建模。多范围注意力层聚合不同范围的邻居信息,学习不同范围的重要性。此外,我们融合 MRA-BGCN 和 RNN 对时间依赖建模完成交通预测。
Bicomponent Graph Convolution
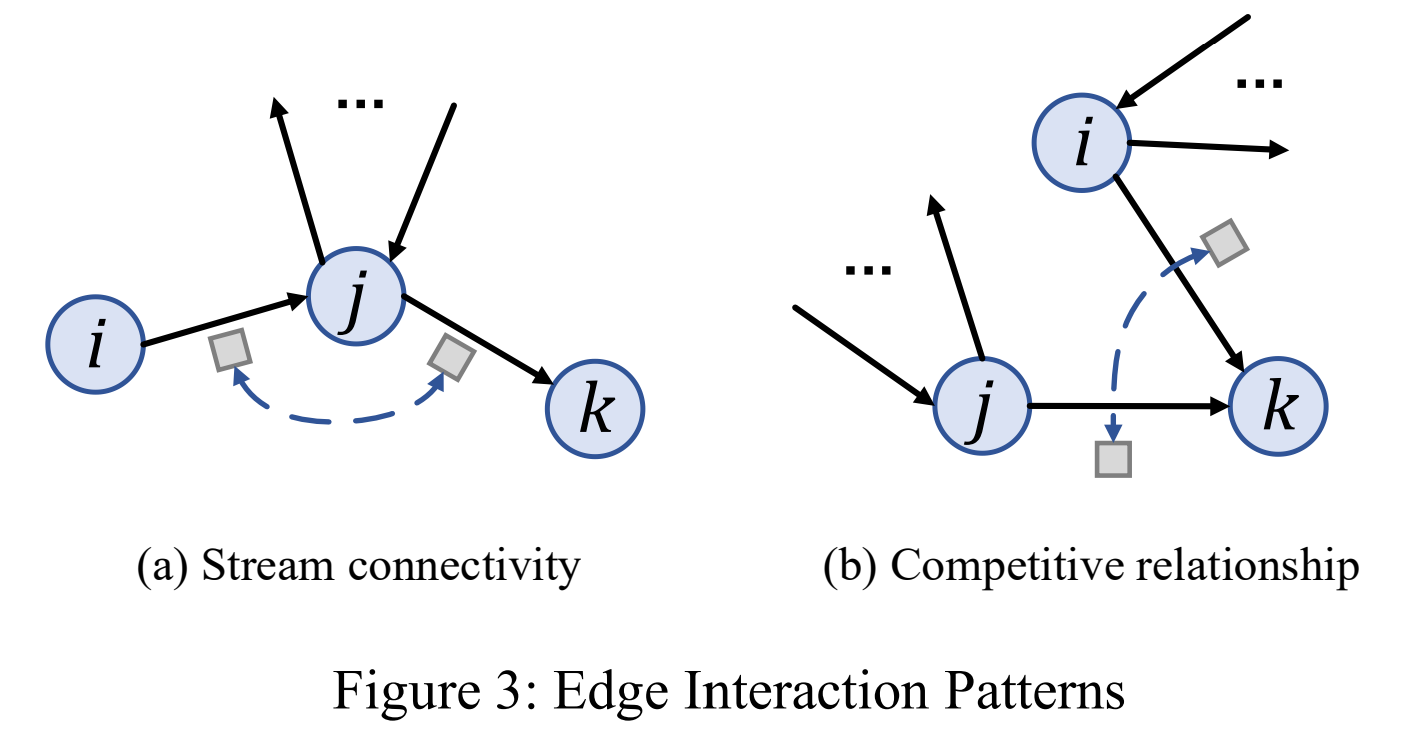
图卷积可以有效聚合结点之间的交互关系,然而,交通预测中边更复杂(这句话说三遍了)。因此我们提出双组件图卷积,直接对结点和边的交互建模。
Chen 等人提出边的邻近的 line graph 来建模边的关系。$G = (V, E, \bm{A})$ 表示结点有向图,$G_L = (V_L, E_L, \bm{A}_L)$ 是对应的 line graph,$G_L$ 的结点 $V_L$ 是 $E$ 中有序的边。$\bm{A}_L$ 是无权的邻接矩阵,编码了结点图中的边邻接关系,有关系就等于1。
尽管 line graph 可以考虑边的邻接,它仍然是一个无权图且只认为两条边中的一条边的汇点和另一条边的源点相同时,这两条才相关。然而,对于刻画交通预测中各种各样边的交互关系来说这不够高效。如图 3 所示,我们定义两类边的交互模式来构建边图 $G_e = (V_e, E_e, \bm{A}_e)$。$V_e$ 中的每个节点表示 $E$ 中的边。
Stream connectivity 在交通网络中,路网可能受它上下游的路段影响。如图 3a 所示,$(i \rightarrow j)$ 是 $(j \rightarrow k)$ 的上游的边,因此他们是相互关联的。直观上来看,如果结点 $j$ 有很多数量的邻居,那么 $(i \rightarrow j)$ 和 $(j \rightarrow k)$ 之间的关系是弱的,因为它还要受其他邻居的影响。我们使用高斯核计算边的权重用来表示 $\bm{A}_e$ 中的 stream connectivity:
$\text{deg}^-(j)$ 和 $\text{deg}^+(j)$ 分别表示结点 $j$ 的入度和出度,$\sigma$ 是结点度的标准差。
Competitive relationship 路网

