Recurrent Marked Temporal Point Processes: Embedding Event History to Vector
KDD 2016: RMTPP Recurrent Marked Temporal Point Processes: Embedding Event History to Vector。经典论文,利用RNN近似条件强度函数,将传统点过程带入到神经点过程。
1. Introduction
当前方法两类变量马尔可夫模型,把问题看作是discrete-time sequence prediction task。基于观察到的状态序列,预测下一步最可能的状态。缺点是这类模型的时间是单位变化的,在预测下一个事件的时候不能捕获时间的heterogeneity。此外,状态不能太多,要不然算不过来,就没法捕获长距离的依赖关系。半马尔可夫模型[26]可以用来建模两个连续事件之间的continuous time-interval,通过假设interval之间是一个简单的分布,但是随着阶数的增加,计算仍然会爆炸。
第二类是marked temporal point processes和intensity function,这两类是建模这种事件数据更通用的数学框架。地震学中,时间点过程广泛用用在建模地震和余震上面。每个地震表示时空空间中的一个点,地震学已经提出不同的公式来捕获这些事件的随机性。金融领域,时间点过程是经济学的活跃方向,可以给出现代金融市场复杂动态性的一些简答解释。
但是实际中典型的这些点过程模型的假设一般做不到,而且这些模型的表达能力有限。我们提出了新的marked时间点过程模型,RMTPP,同步建模事件的事件和标记。我们方法的核心是将一个时间点过程的intensity function看作是一个历史过程的非线性函数,这个函数用RNN表示。
2. 问题定义
一组序列 $\mathcal{C} = \{ S^1, S^2, \dots, \}$
序列 $\mathcal{S}^i = ((t^i_1, y^i_1), (t^i_2, y^i_2), \dots)$ 是$(t^i_j, y^i_j)$组成的序列,$t^i_j$是事件发生的时间,$y^i_j$是事件的类别。
- 给定实体$i$,预测下一个事件pair $(t^i_{n+1}, y^i_{n+1})$
- 计算一个给定序列的likelihood
- 通过学习得到的模型模拟一个新的序列
3. Related Work
现存工作的一个主要的限制就是对latent dynamics的各种参数假设,latent dynamics控制了观测到的点过程的生成。
4. Marked Temporal Point Process
这个第四节主要介绍了之前的一些点过程使用的条件强度函数。
标记时间点过程是一个对观测到的随时间发生的随机事件模式进行建模的强有力工具。因为一个事件的出现与历史发生了什么有关,我们可以指定一些模型,给定我们已知的过去,对下一个事件建模。严格来讲,一个标记时间点过程是一个随机过程,这个随机过程包含了一个带有时间信息的离散事件的列表,$\{ t_j, y_j \}$,$t_j \in \mathbb{R}^+, y_j \in \mathcal{Y}, j \in \mathbb{Z}^+$,$t$是时间,$y$是标记。历史 $\mathcal{H}_t$ 是直到时间$t$的事件时间和标记组成的list。连续事件时间之间的时间差 $d_{j+1} = t_{j+1} - t_j$ 称为事件间的duration。
给定过去事件的历史,我们可以指定下一个事件类型$y$在时间$t$发生的条件密度函数为 $f^{\ast}(t, y) = f(t, y \mid \mathcal{H}_t)$,$f^{\ast}(t, y)$强调了这个密度是基于历史的这个条件。利用链式法则,可以得到一个序列的联合似然为:
$f^{\ast}(t_j, y_j)$ 有很多种形式可以选择。但是实际中人们一般选择非常简单可分解的形式,比如$f(t_j, y_j \mid \mathcal{H}_t) = f(y_j) f(t_j \mid \dots, t_{j-2}, t_{j-1})$,要不然对事件标记和时间进行联合建模会非常复杂。我们可以认为在$y_j$只可取有限个值且与历史完全无关的时候,$f(y_j)$是一个多项式分布。$f(t_j \mid \dots, t_{j-2}, t_{j-1})$是给定过去事件的时间的序列时,事件发生在$t_j$的条件密度。而且需要注意的是,$f^{\ast}(t_j)$不能捕获过去事件标记的影响。
4.1 Parametrizations
一个标记点过程的时间信息可以通过一个典型的时间点过程来捕获。一个刻画时间点过程的重要方式是通过条件强度函数——给定过去所有事件,对下一个事件建模的随机模型。在一个小的时间窗口$[t, t + dt)$里,$\lambda^{\ast}(t)dt$是一个新事件在给定历史$\mathcal{H}_t$时出现的概率:
$\ast$是用来提醒我们这个函数是依赖历史的。给定条件密度函数$f^{\ast}(t)$,条件强度函数为:
$F^{\ast}(t)$是在最后一个事件时间$t_n$之后,一个新事件发生在$t$之前的累积概率,$S^{\ast}(t) = \text{exp}(- \int^t_{t_n} \lambda^{\ast}(\tau) d\tau)$ 是$t_n$到$t$之间没有新事件发生的概率。因此条件密度函数可以写成:
5. Recurrent Marked Temporal Point Process
条件强度函数的形式决定了一类点过程的事件性质。但是,为了考虑marker和事件信息,在缺少前沿知识的情况下很难决定使用哪种形式的条件强度函数。为了解决这个问题,作者提出了一个统一的模型,可以在历史的事件和marker信息上对非线性依赖建模的模型。
5.1 Model Formulation
公式5,6,7有不同的表达形式,而且是对过去事件不同类型的依赖结构。受到这一点的启发,我们希望能学习到一个趋近于历史未知依赖结构的通用表示。
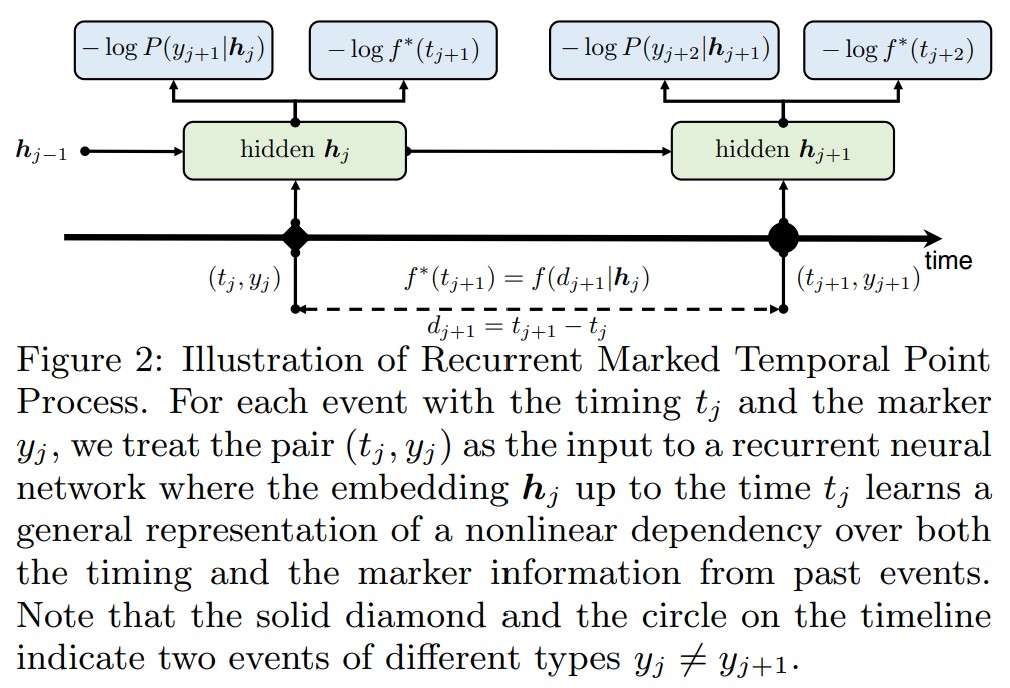
我们的想法是用RNN来实现这一步。如图2所示,RNN在时间步$t_j$的输入是$(t_j, y_j)$。$y_i$是事件的类型。$h_{j-1}$表示从过去事件和事件得到的影响的memory,在更新的时候会考虑当前的事件和时间。因为$h_j$表示过去一直到第$j$个事件的影响,那么下一个事件时间的条件强度函数就可以表示为:
$d_{j+1} = t_{j+1} - t_j$。因此,我们可以用$h_j$去预测时间$\hat{t}_{j + 1}$和下一事件类型$\hat{y}_{j + 1}$。
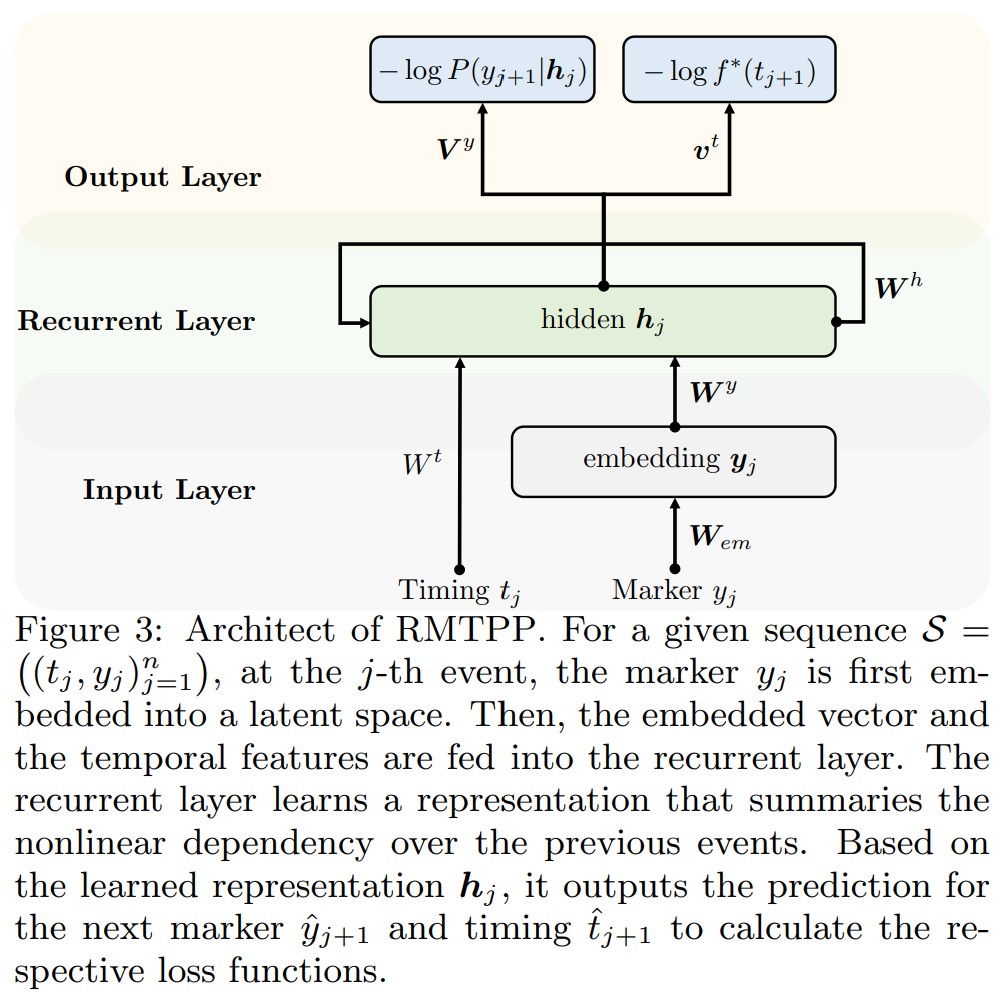
这个公式的好处是我们将历史事件嵌入到了一个隐向量空间,然后通过公式4,我们不用指定一个固定的参数形式来建模历史的依赖结构,可以用一个更简单的形式得到条件强度函数$\lambda^{\ast}(t)$。图3展示了RMTPP模型的架构。给定一个事件序列$\mathcal{S} = ((t_j, y_j)^n_{j=1})$,通过迭代以下组件,得到一个隐藏单元$\{ h_j \}$的序列。
Input Layer,先用一个input layer对one-hot的事件表示进行投影。$y_j = W^T_{em} y_j + b_{em}$。然后事件步$t_j$也投影成一个向量$t_j$。
Hidden Layer
Marker Generation,给定表示$h_j$,我们用一个多项式分布建模marker的生成:
$K$是marker的个数,$V^y_{k,:}$是矩阵$V^y$的第$k$行。
Conditional Intensity,基于$h_j$,可以得到条件强度函数:
$\mathcal{v}^t$是一个列向量,$w^t, b^t$是标量。
- 第一项 $\mathcal{v}^{t^T} \cdot h_j$ 表示过去的事件和时间信息累积的影响。对比公式5,6,7对过去影响固定的公式,现在这个是对过去影响的高度非线性通用表示。
- 第二项强调当前事件$j$的影响。
- 最后一项对下一个事件的出现给了一个基础的强度等级。
- 指数函数是一个非线性函数,且保证强度永远是正的。
通过公式4,我们可以得到给定历史的情况下,下一个事件在时间$t$出现的likelihood:
然后,下一个事件的时间可以用期望来计算
一般来说,公式13的积分没有解析解,我们可以用[32]的用于一维函数的数值积分技术来计算公式13。
Remark。因为我们用RNN表示历史,所以条件强度函数$\lambda^{\ast}(t_{j+1})$的公式11,捕获了过去事件和时间两部分信息。另一方面,因为marker的预测也依赖于过去的时间信息,当时间和事件信息相互关联的时候,就可以提升模型的性能。后面的实验证明了这种互相提升的现象确实存在。
5.2 参数学习
最大对数似然
$\mathcal{C} = \{ \mathcal{S}^i \}$是一组序列, $\mathcal{S}^i = ((t^i_j, y^i_j)^{n_i}_{j=1})$。用BPTT训练。

